長桝網代編みの横の(小さい方の)四角数については、
- その数で立ち上げ位置が(上の四角/中の四角/下の四角)が決まる
- いずれの位置でも立ち上げ可能
- 従って、横の四角数はいくつでもよい
ということがわかりました。
次は、縦の(大きい方の)四角数です。この数については、いくつでも良さそうです。
試しに、横の四角数を14としてすべて同じにし、縦の四角数を32~15の間で少しづつ変えた絵を作ってみました。
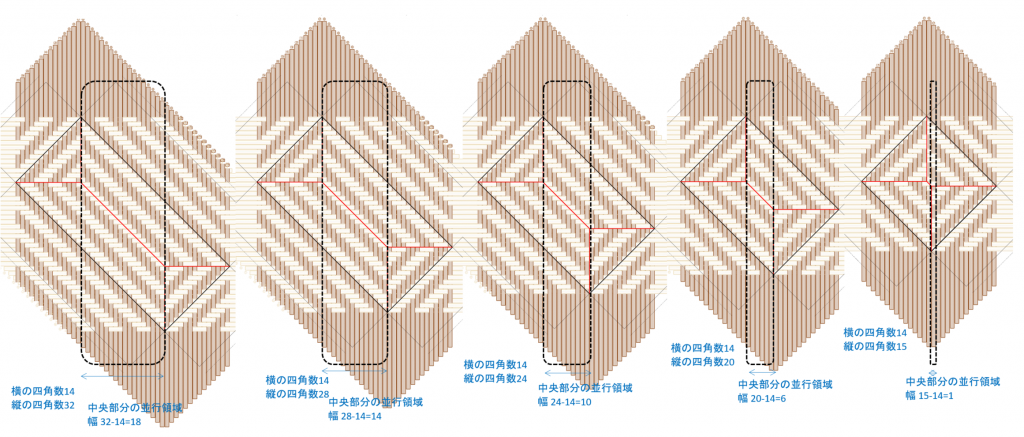
絵を並べてみると、それぞれの底が、2つの部分で出来ているのが読み取れるでしょうか。この2つの部分についてまとめたのが下の表です。
| 呼び名 | 表示と形状 | 編み目 | 縦の四角数(32~15)との関係 |
|---|---|---|---|
| 角(かど)にかからない中央部分 | 黒の点線(角丸四角)で囲まれた中、平行四辺形 | 3つ飛び網代編みが平行に並ぶ | 高さは、すべて同じ 幅は、縦マイナス横 |
| 角(かど)の三角形部分 | 黒の点線の外側、左側と右側、各二等辺三角形 | (上図は仮・次節で説明) | すべて同じ |
表の「縦の四角数(32~15)との関係」欄にまとめていますが、横の四角数が同じであれば「角にかからない中央部分」の高さ、および「角の三角形部分」の形状は、縦の四角数によらず同じです。縦の四角数の影響を受けるのは「角にかからない中央部分」の幅だけです。
「角にかからない中央部分」の幅は、縦の四角数から横の四角数をマイナスした数です。そしてこの幅の値は、いくつにでも作ることができます。ということは、縦の四角数も、いくつにでも作れる、ということです。横の四角数で決まる三角形部分とは無関係に。
そして最後に、残りの「角の三角形部分」を見てみましょう。上の図ではまだ仮の絵で、横の四角数によって決まる立ち上げ位置(上の四角/中の四角/下の四角)だけが合っている状態です。これを、「長桝網代編み」の
- 飛び数は、1,3,5でできている
- 3つ飛び模様は長方形に繋がっている
- その長方形は入れ子になっている
のように作れるのでしょうか。
以下の図は、上図の右から2点目、14×20の図です。赤の中央線のところに不連続な並びがありますが、三角の内側(角側)2本分をグレーの帯でマスクしてみました(元がわかるよう少し透過性を持たせています)。
マスクされた状態で全体を眺めてみると、つながった、入れ子の長方形が見えてきませんか?それに、ベースが3で出来ていますから、1,3,5でつながりそう、ですよね。
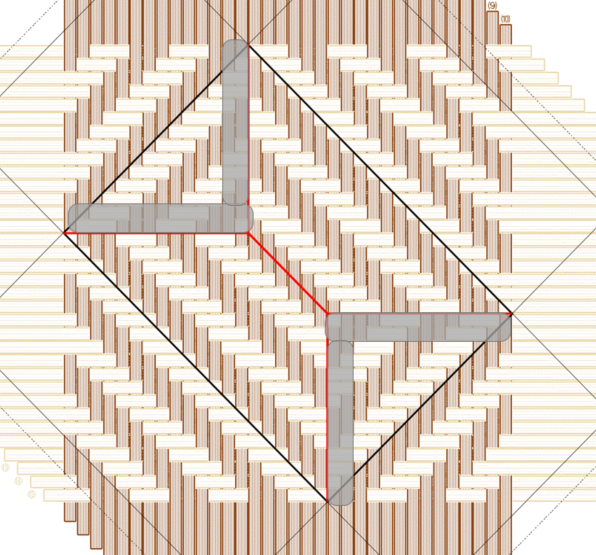
つながりのちょっとした入れ替え、マッチ棒クイズみたいだと思いませんか?