長方形の底で、長方形が入れ子に重なっている長桝網代編み、今まで作ったのは文献に記載されていた14×32、そしてその同じ模様を使ったものです。
でも、その数でないと作れないなんていうことはないはず。では、縦と横、どんな本数でも作れるのでしょうか。それとも、特定の決まった数でないと作れないのでしょうか。検討してみました。
まず、任意数の四角が縦に並んでいるとします。それを、上端・下両から3つごと、上下対称に塗りつぶしていくとします。中央部に最後に残るのは、下図の黄色の四角、5・4・3・2・1・0個のいずれかです。
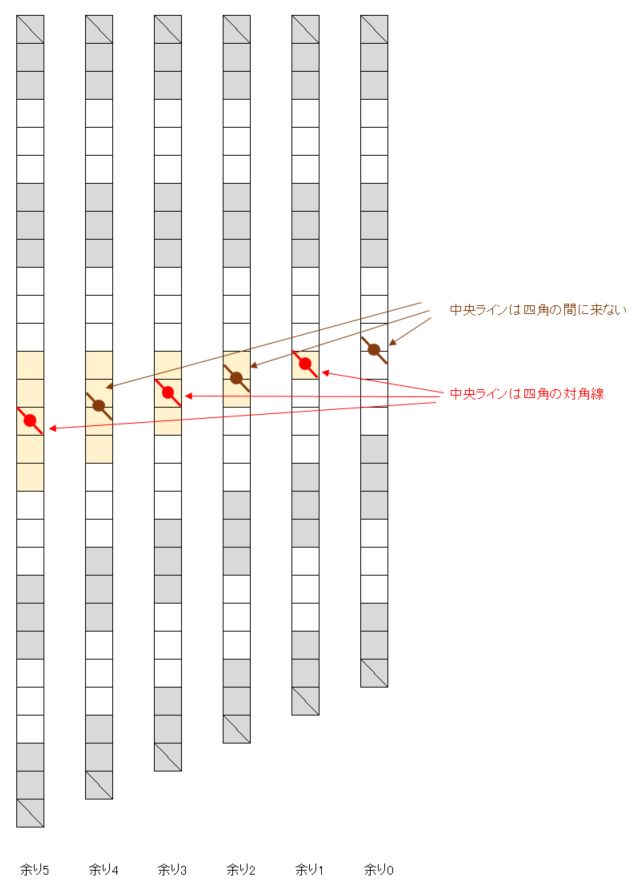
この縦に並ぶ四角を、長桝網代編みの中央部分(下図の点線部分)に適用してみましょう。3つごと=3つ飛び網代編みです。立ち上げは四角の対角線で折りますので、中央となるラインも対角線に来ます。従って、余りが0,2,4にはなりません(上図の茶色)。中央に残るのは、1か3か5 です。
下図、左から余り3・余り1・余り5の例です。任意の数を任意の位置の3つ飛びで埋めた場合、いずれかになるということです。
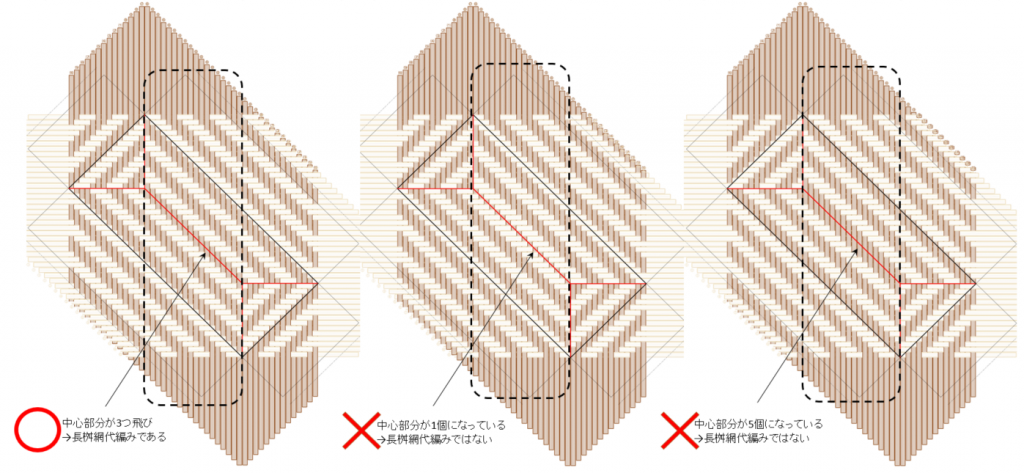
このうち「長桝網代編み」と呼べるのは、余りが3となる左側のケースのみでしょう。いずれも1,3,5 で出来ているとはいえ、角以外は3つ飛びが基本でしょうから。
では次に、この長桝網代編みの中央部分の数は何で決まるのでしょうか。
下図のように、横の四角数の角の部分は、直角二等辺三角形で作られていますので、中央部分の高さは横の四角数の2倍、そこに立ち上げ位置の四角がプラス1です。

上図に従った式を作ると、
- ((横の四角数×2+1) -3) を6で割った余りが、(1 + 1)の時、下の四角
- ((横の四角数×2+1) -3) を6で割った余りが、(2 + 2)の時、中の四角
- ((横の四角数×2+1) -3) を6で割った余りが、ゼロの時、上の四角
6で割った余りが0/2/4ということですが、1/3/5になることはないのでしょうか。
はい、×2で偶数、+1-3しても偶数ですから、余りも偶数です。
もうすこし式を整理すると、横の四角数と立ち上げ位置との関係は
- 横の四角数 を3で割った余りが2の時、下の四角
- 横の四角数 を3で割った余りがゼロの時、中の四角
- 横の四角数 を3で割った余りが1の時、上の四角
先の文献『竹細工 増補改訂版』の長桝網代編みの作例は14と11でした。「横の四角数 を3で割った余りが2」となる数が該当します。たぶんこの数が、いちばん作り易いのでしょう。
※「横の四角数」としていますが、正確には横の四角数と縦の四角数のうち、小さい方の四角数です。縦の四角数の方が小さいときは、左右に反転した絵になります。