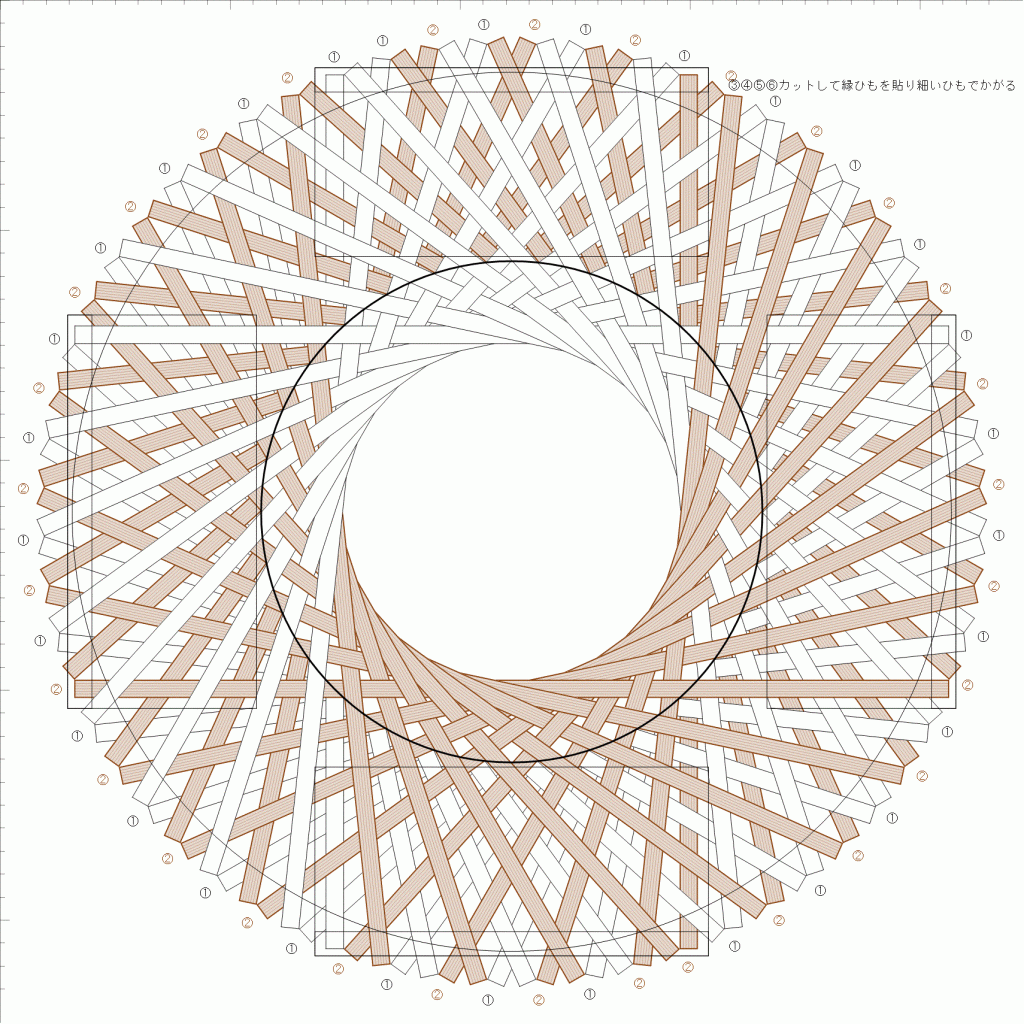
ということで、同じサイズで、飛び数(連続数)を 5-1 にしたかごを作ってみました。先と同じ3色の輪弧ですが、合わせる位置を2本分ずらした、ちょっと違う模様です。

5-2 の時に比べると、輪の部分からの編み目も自然ですし、底板も固定されました。

底、つまり立ち上げ位置でサイズが決まりますが、側面を詰める想定なので「底の周に対するひも幅の割合」の値がほぼ50%となる設定です。上の写真を見ても、折り位置が、重ならずに一番詰まった状態になっています。
でも、側面は詰め切れずにすき間が空いているので、その分広がっています。Square45で試算してみると、すき間0.5mmにつき周が4cm強増えますので、サイズ的にもほぼその位(しかもランダムに..)かな、という感じです。
プレビュー図です。

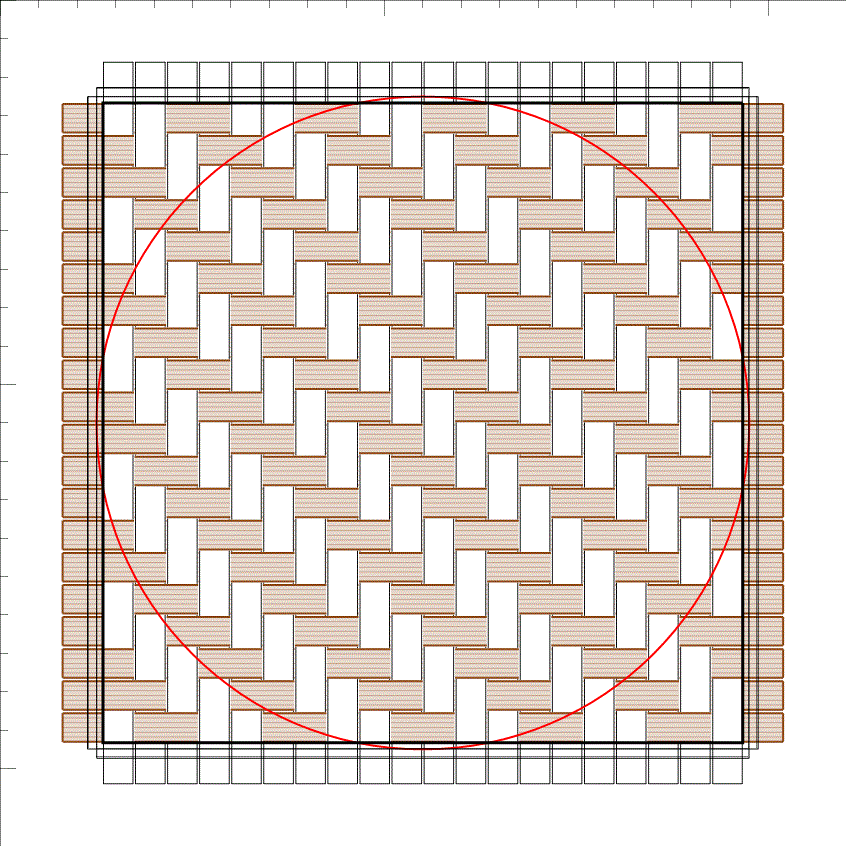
底板です。

CraftBandMesh V1.8.12 のデータです。
CraftBandSquareのデータです。