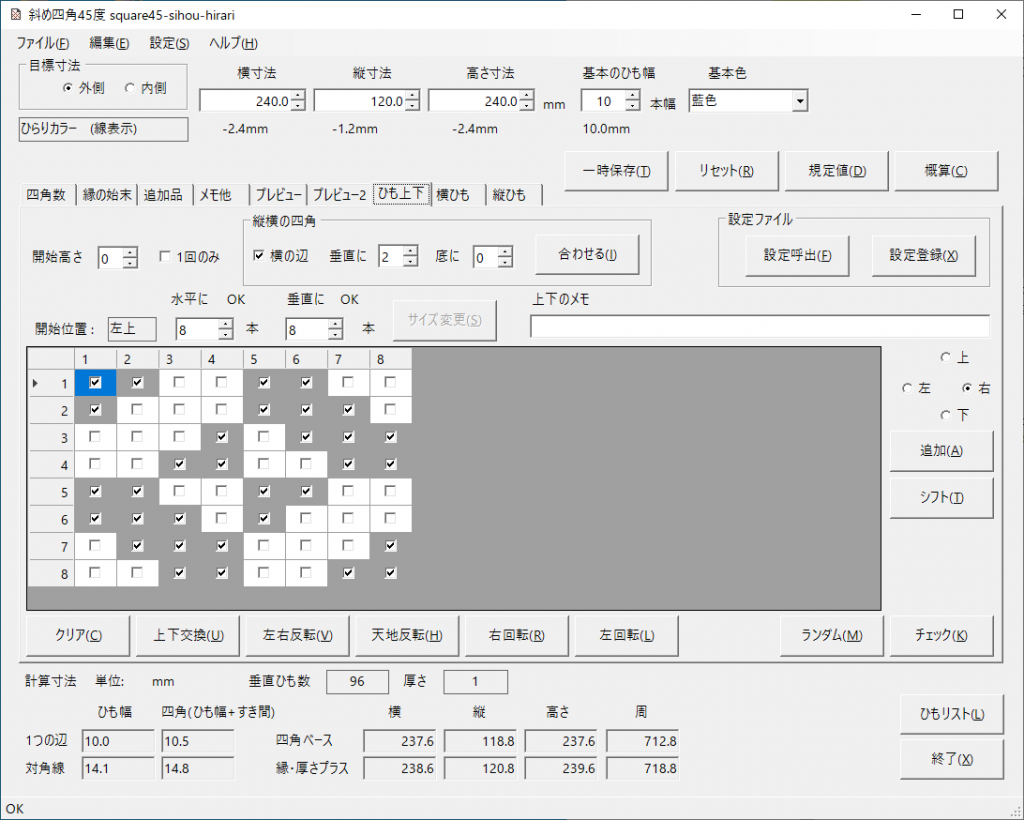
斜め編みで外側・内側ともにクロスになる配置として、今まで交色ベースで試してきましたが、縦横に色を切り替えた非対称のパターンでも折り返しが可能です。
横の四角数8・縦の四角数3で、切り替え位置を縦横の四角数に合わせて作ってみた例です。
前面と背面に、最小と最大のクロス領域が作られています
※前と後ろの模様が異なります
大きい方のクロス領域を、外側に折りカラー編みして底で始末します
※逆でも可ですが外側の方処理しやすい為
残りの小さい方のクロス領域を、内側に折りカラー編みします
※底の始末は内側を先にした方がよいかも
全体がクロスになりました
※底は、外側・内側とも、「底の中央線」まで差し込みました
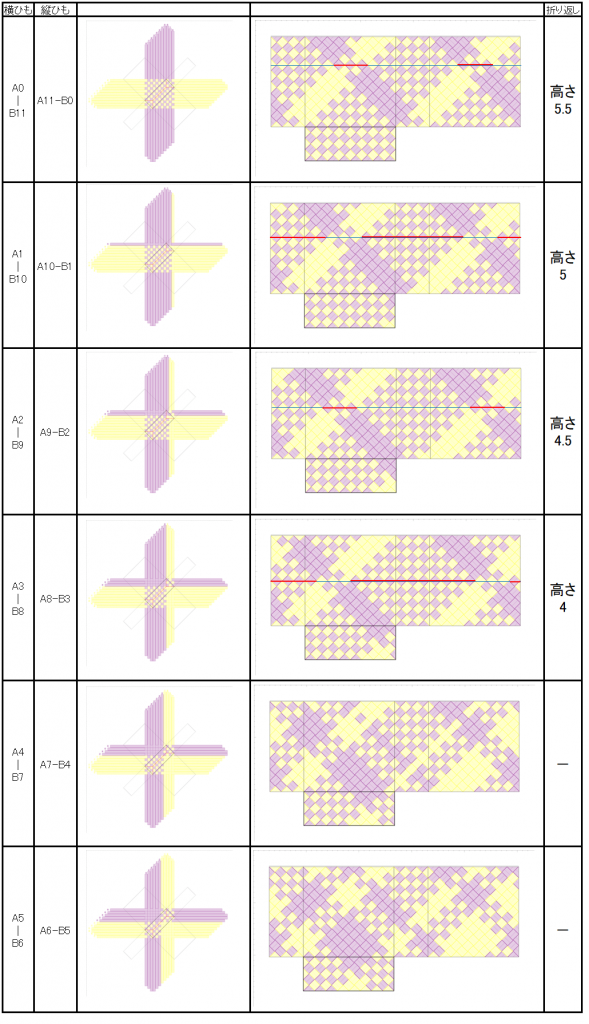
この例では、縦ひも・横ひもとも11本です。A,B2色で、Aが紫,Bがピンクとして、交色から半分の5-6までの配置パターンの組み合わせをリストアップすると、次の図のようになります。5-6に続く6-5以降は、縦横を入れ替えたものに相当しますので、配置パターンとしては全てになります。
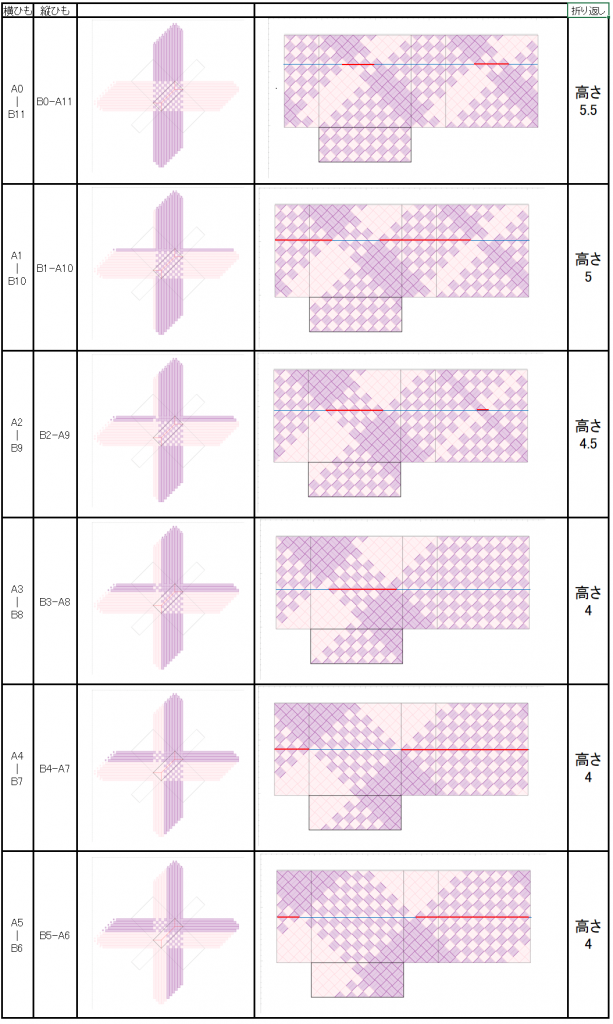
縦ひも・横ひもを2色を切り替えて配置し、縦横で色を逆にした場合は、図から、
- 切り替え位置によらず、折りカラー編みでクロスにすることは可能
- 同色本数のいずれかが縦の四角数(小さい方)より小さければ、折り返し位置はクロス2箇所で、高さは 「同色本数の多い方/2」
- 同色本数が共に縦の四角数(小さい方)以上であれば、折り返し位置はクロス1箇所で、高さは 「横の四角数(大きい方)/2」
- 高さは 「横の四角数(大きい方)/2」~「(横の四角数+縦の四角数)/2」 [+(横の四角数+縦の四角数)の整数倍]で、0.5単位
交色から開始した場合より高さの調整範囲は狭くなりますが、小数点以下ゼロと0.5 が選べますし、前後非対称な位置を選ぶことができます。
試作例のデータです。A3-B8 ・高さ4のパターンです。