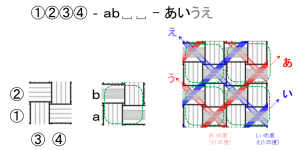
レベル2-クロスベース模様のカテゴリー
さて、ここまで、レベル1のステッチ、および2015年までの書籍に見られたステッチを見てきました。続いて、2021年頃からの再ブーム以降の書籍に見られるパターンを見ていこうと思います。
近年の書籍に掲載されている作品は、バンド色や後差し配置を複雑に組み合わせてデザインされていますが、その構成要素を分解し、「単位となる模様」だけを取り出してみると、多くは「クロス模様」構造——すなわち、水平ないし垂直に通したレベル1のバンドに、45度・135度方向でレベル2のバンドを通すタイプ——をベースとしていることが分かります。
編み方や差し方そのものは共通であり、バンドの色構成によって違いを生み出している点は、編み組織そのもののバリエーションを作ってきた伝統的なかごとは異なる方向性です。これは、カラフルなPPバンドという現代素材ならではの装飾的展開といえるでしょう。また後差しについても、当初は固定する感覚が強かったものが、差し込むだけで十分に保持され問題ないことが経験的に理解されてきた結果、より自由に用いられるようになってきたと考えられます。
クロス模様をベースとした模様を分析するにあたり、単位全体のサイズは 4×4 とします。基本となるレベル0とレベル1は 2×2 単位としますが、クロスするレベル2構造は 2×2 には各方向1点しか存在しません。そのため、最小の組み合わせとして縦横2倍の領域、つまり 4×4 を単位として整理しています。
▼ 模様の単位と条件
- 使用色:A色・B色の2色
- レベル1:水平方向の2本(※垂直方向については転置扱い)
- レベル2:45度・135度方向ともに同じ配色の2セット
- 単位サイズ:
- 模様全体の単位は 4×4
- ただし、ベース(レベル0,1)は 2×2 単位の繰り返し
▼ 模様コードによる分類
レベル1の時と同様に、色並びのコードを使って分類します。
先には「(レベル0:ベース) – (レベル1:縦横)」の構成でしたが、今回は、レベル1は片方向のみ、レベル2の斜め方向が加わるため、コードは以下のような構成になります。
(レベル0:ベース 4文字)-(レベル1:縦 2文字)-(レベル2:斜め 2/4文字)
- レベル0, レベル1部分については先と同じで、レベル1部分の後半が空白なら詰めます。
- レベル2部分は、斜め方向2箇所で、45度と135度が同色の場合は2文字に省略します(ABAB→AB)。
▼ ベース(レベル0)のカテゴリー
A色・B色の反転や回転・対称性を考慮して、以下の6点をベースにします。
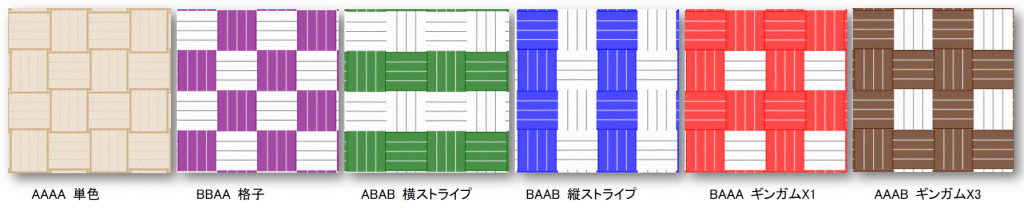
- AAAA 単色
- BBAA 格子
- ABAB 横ストライプ(レベル1と同方向)
- BAAB 縦ストライプ(レベル1と直交方向)
- BAAA ギンガムX1(1/4色でクロス)
- AAAB ギンガムX3(3/4色でクロス)
これらをカテゴリーとして、順に、そのカテゴリーに属する模様をみていきたいと思います。
PPバンド・重ね菱模様のステッチ
| 名称 | 重ね菱(かさねびし)模様 | Overlapping Diamond Pattern |
| 概要 | クロス模様+菱模様 | AAAA-BBS23-C |
| 単位 | [水平方向] 2 | [垂直方向] 6 |
| レベル0 | [水平] A色 | [垂直] A色 |
| レベル1 | [水平] B色(1/4幅) | [72度] 0: – | 1:C色(1/2幅) [108度] 0: – | 1:C色(1/2幅) |
| レベル2 | [45度] 0: – | 1:B色(1/4幅) | [135度] 0: – | 1:B色(1/4幅) |
| 備考 | 72度・108度は、45度・135度にover | 転置 レベル1方向 |
富田淳子 (2015). 『PPバンドで作るベトナムのプラカゴ』 文化出版局.
66-67ページ、作品29「幾何学模様のバッグ」からです。
A色が赤、B色が白、C色がミントグリーンです。
レベル2のクロス模様を作った後、レベル1の菱模様を加えています。「幾何学模様」では漠然としすぎるので、構造を反映して「重ね菱」としました。

持ち手のない収納かごですので、非対称でも問題になりません。縦ひも・横ひもとも偶数にしてみました。
内側と底です。ステッチは側面だけです。
1単位分の編み目(青枠)です。後から差した、72度+108度のバンドについては、上に重ねる図(左図)になっていますが、実際はベースのバンドに差し込みます(右写真)。

※前側面の左下から、右(0度)方向・上(90度)方向にカウントアップ。左下は垂直方向がover/水平方向がunderです。
Squareのデータです。
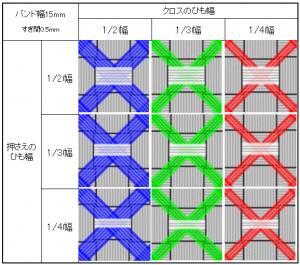
後差しひもの幅 : 1/2, 1/4 そして 1/3へ
最初のレベル2ステッチ「クロス模様」では、以下の幅のバンドを使用しています。
- レベル1:1/2幅
- レベル2:1/4幅
なぜこの組み合わせになったのか、その理由を当時の背景とともに紐解いてみましょう。
まず、土台となる「レベル1」についてです。既に持ち手などに1/2幅のバンドが使われていましたから、レベル1に同じ1/2幅を採用するのは自然な流れでした。
次に、そこに重ねる「レベル2」がなぜ1/4幅なのかという点です。これにはスペースと道具という2つの理由があります。
物理的なスペースの問題として、1/2幅で埋まっている場所に、斜め方向からさらに同じ1/2幅を通す余裕はありません。必然的に、それよりも細いバンドが必要になります。
そしてもう一つは、2014年当時の道具の事情です。 当時はハサミや自作の道具でカットしていたため、正確に3等分(1/3幅)にするのは難しかったでしょう。一方で、バンドを半分に折ってカットするのは簡単です。つまり、1/2幅をさらに半分にした1/4幅を作るのが、手作業において最も合理的で確実な方法だったのです。
しかし、現在は状況が異なります。 2023年から2024年にかけて、PPバンドを簡単に等幅に割ける、PPバンドカッターなどと呼ばれる専用ツールが発売されたからです。これにより、以前は難しかった「1/2幅」「1/3幅」「1/4幅」といった細かい調整も、誰もが手軽に行えるようになりました。
では、道具の進化により「1/3幅」という選択肢が加わった現在、実際にどのような組み合わせが可能なのでしょうか。
まずは、数値的な側面から検証してみましょう。 15mm幅のPPバンドを使用した場合、ベースとなる「押さえのひも(レベル1)」と、斜めに通す「クロスひも(レベル2)」の間に、どれくらいのスペースがあるかを計算したのが下の図です。
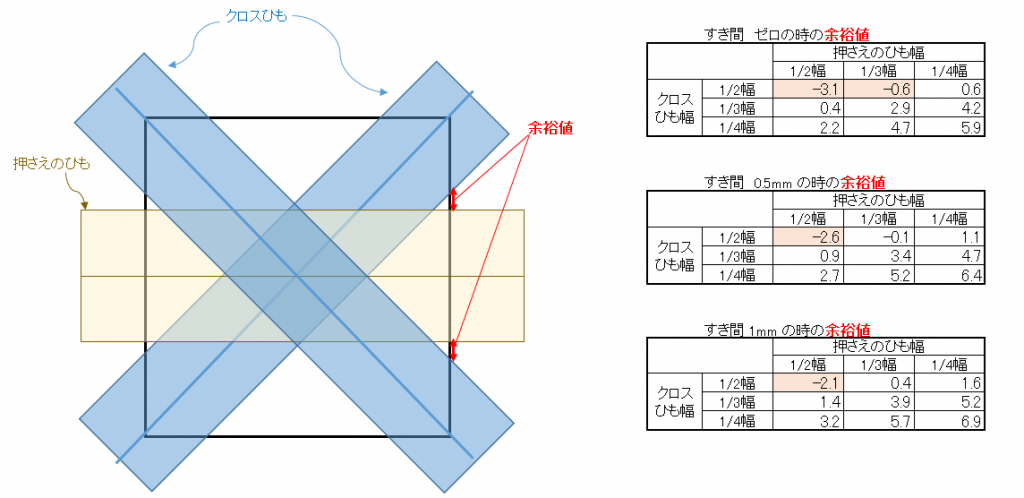
表の数値は、バンド同士の「余裕値」を示しています。これがマイナスになっている箇所は、物理的にスペースが足りずひもが重なる、つまり通らないことを意味します。プラスであっても、小さければ通しにくい。また、大きすぎる場合は可動領域が広い、つまりずれやすいことを意味します。
この数値だけではイメージしづらいかもしれませんので、バンド間のすき間を0.5mmに設定した状態を、図で可視化してみましょう。
「1/2幅」のベースに対して、「1/4幅」は通しやすくずれにくい絶妙な値です(上段・右列)。でも同じ「1/2幅」をクロスさせようとすると、大きく重なってしまい通すことができません(上段・左列)。
一方で、これまで難しかった「1/3幅」であれば、1/2幅のベースに対してもなんとか通すことができます。さらに、「1/3幅 × 1/3幅」同士の組み合わせ(中段・中央列)であれば、従来の「1/2幅 × 1/4幅」と同じような感覚で、無理なく通せることがわかります。
では、実際に作品にした場合、見た目はどう変わるのでしょうか?
最もポピュラーな「花模様」を例に、3つのパターンを比較してみます。

左から順に以下の組み合わせです。
- 左:1/2幅 × 1/4幅(従来の基本スタイル)
- 中:1/3幅 × 1/3幅(均等なバランス。柔らかな印象)
- 右:1/4幅 × 1/2幅(クロスを太くした逆パターン。明確な分離)
※画像ではレベルごと同じ幅にしていますが、色ごとに幅を変えればさらに表情が変わります。
長らく「1/2幅 × 1/4幅」が基本とされてきましたが、それは絶対的なルールではありません。 道具が進化し、選択肢が増えた今、作りたい模様の雰囲気や好みに合わせて、ひも幅の組み合わせも選べるのではないでしょうか。
PPバンド・クロス模様のステッチ
| 名称 | クロス模様 | Crisscross Pattern |
| 概要 | 単色ベース、斜めクロス1色 | AAAA-BB-C |
| 単位 | [水平方向] 2 | [垂直方向] 2 |
| レベル0 | [水平] A色 | [垂直] A色 |
| レベル1 | [水平] B色(1/2幅) | |
| レベル2 | [45度] 0: – | 1:C色(1/4幅) | [135度] 0: – | 1:C色(1/4幅) |
| 備考 | B色とC色が同じ場合も含む | 転置 レベル1方向 |
古木明美 (2014). 『PPバンドで作る かわいいプラかごとバッグ』 河出書房新社.
37ページ、「赤×白ステッチのバスケット」からです。白が “クロスひも” として表現されていますので、クロス模様としました。
レベル1のB色が赤、レベル2のC色が白です。白のクロスひもを、赤のレベル1ひもで支える、レベル2構造の模様となります。

内側と底です。内側はベース一色です。模様は側面のみなので、底もベース色です。
1単位分の編み目(青枠)です。

※前側面の左下から、右(0度)方向・上(90度)方向にカウントアップ。左下は垂直方向がover/水平方向がunderです。
Squareのデータです。
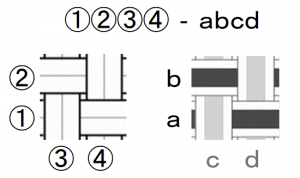
レベル1-縦横ステッチのバリエーション
これまで、窓模様や梁模様など、ベースに対して縦横にひもを差すパターンをいくつか試作してきました。いずれも平編みの「2×2単位」に「2色(A/B)」です。この最小条件において、他にどのような模様があるのか、組み合わせ画像を作ってみました。
条件は以下の通りです。
- レベル0 – ベースの柄: 単色 / 格子 / ストライプ / ギンガムチェック
- レベル1 – 後差しひも: 水平ひも・垂直ひも、ともにA色もしくはB色
実際にかごをデザインする際は、全体としての色並びや差し位置をつくりますが、部分を構成する「単位(ユニット)」にどのような図柄があるのか。 そのバリエーションが「模様のカタログ」としてリストアップされていれば、参考になるでしょう。
※実のところ、リストアップしながら、え?こんなにあったの?と思いました。でも、改めて考えれば、4×4×4×4ですからむしろ当たり前の数。やってみるものですね。
単色ベースのステッチ
※A色ベース。シフトした図柄のみをまとめ、転置した図柄は別扱いとしています。
| 水平ひもの並び(↑) | 垂直ひもの並び(→) | パターン | コード / 名称 |
|---|---|---|---|
| AA | AA |  | AAAA-AAAA |
| AA AA | AB BA |  | AAAA-AAAB AAAA-AABA |
| AA | BB |  | AAAA-AABB |
| AB BA | AA AA |  | AAAA-ABAA AAAA-BAAA |
| AB | AB |  | AAAA-ABAB |
| AB BA | BA AB |  | AAAA-ABBA AAAA-BAAB |
| AB BA | BB BB |  | AAAA-ABBB AAAA-BABB |
| BA | BA |  | AAAA-BABA |
| BB | AA |  | AAAA-BBAA |
| BB BB | AB BA |  | AAAA-BBAB AAAA-BBBA |
| BB | BB |  | AAAA-BBBB 井桁(いげた)模様 Grid Pattern |
格子ベースのステッチ
※格子のABを入れ替えると、転置した図柄になります。
| 水平ひもの並び(↑) | 垂直ひもの並び(→) | パターン | コード / 名称 |
|---|---|---|---|
| AA | AA |  | BBAA-AAAA |
| AA AA | AB BA |  | BBAA-AAAB BBAA-AABA |
| AA | BB |  | BBAA-AABB 梁(はり)模様 Beams Pattern |
| AB BA | AA |  | BBAA-ABAA BBAA-BAAA |
| AB BA | AB BA |  | BBAA-ABAB BBAA-BABA |
| AB BA | BA AB |  | BBAA-ABBA BBAA-BAAB |
| AB BA | BB BB |  | BBAA-ABBB BBAA-BABB |
| BB | AA |  | BBAA-BBAA |
| BB BB | AB BA |  | BBAA-BBAB BBAA-BBBA |
| BB | BB |  | BBAA-BBBB |
ストライプベースのステッチ
※横ストライプのリスト。縦ストライプについては転置&シフトした図柄となります。
| 水平ひもの並び(↑) | 垂直ひもの並び(→) | パターン | コード / 名称 |
|---|---|---|---|
| AA | AA |  | ABAB-AAAA 窓(まど)模様 Windowpane Pattern |
| AA | AB |  | ABAB-AAAB |
| AA | BA |  | ABAB-AABA |
| AA | BB |  | ABAB-AABB |
| AB | AA |  | ABAB-ABAA |
| AB | AB |  | ABAB-ABAB |
| AB | BA |  | ABAB-ABBA |
| AB | BB |  | ABAB-ABBB |
| BA | AA |  | ABAB-BAAA |
| BA | AB |  | ABAB-BAAB |
| BA | BA |  | ABAB-BABA |
| BA | BB |  | ABAB-BABB |
| BB | AA |  | ABAB-BBAA |
| BB | AB |  | ABAB-BBAB |
| BB | BA |  | ABAB-BBBA |
| BB | BB |  | ABAB-BBBB |
ギンガムチェックベースのステッチ
※左下が1のリスト。隣が1の場合は、転置&シフトした図柄となります。
| 水平ひもの並び(↑) | 垂直ひもの並び(→) | パターン | コード / 名称 |
|---|---|---|---|
| AA | AA |  | BBAB-AAAA 連窓(れんまど) Linked Window Pattern |
| AA | AB |  | BBAB-AAAB |
| AA | BA |  | BBAB-AABA |
| AA | BB |  | BBAB-AABB |
| AB | AA |  | BBAB-ABAA |
| AB | AB |  | BBAB-ABAB |
| AB | BA |  | BBAB-ABBA |
| AB | BB |  | BBAB-ABBB |
| BA | AA |  | BBAB-BAAA |
| BA | AB |  | BBAB-BAAB |
| BA | BA |  | BBAB-BABA |
| BA | BB |  | BBAB-BABB |
| BB | AA |  | BBAB-BBAA |
| BB | AB |  | BBAB-BBAB |
| BB | BA |  | BBAB-BBBA |
| BB | BB |  | BBAB-BBBB |
なお、編み目については、左下は垂直方向がover/水平方向がunderで固定です。
コードは、「(レベル0:4文字) – (レベル1:4文字)」のような形式で、以下の順で対応する色(A/B)が入ります。
コードで編み方が決まります。反転・回転した図柄を作りたければ、元のコードを指定して、AIに変換を依頼すると良いでしょう。