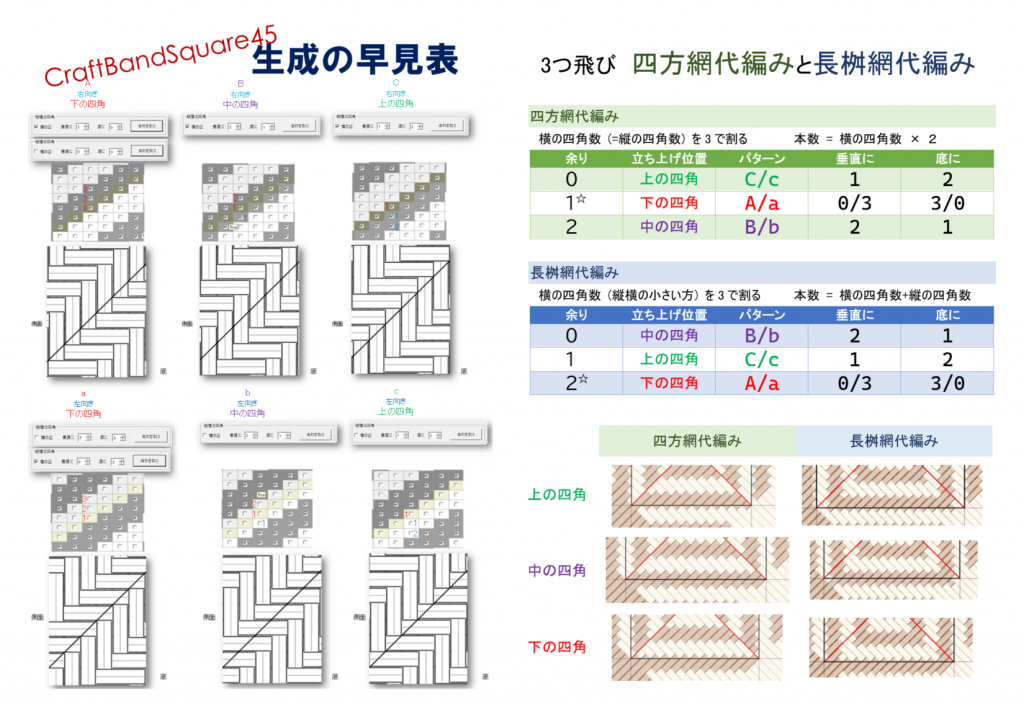
長桝網代編み・四方網代編みは、3つ飛び網代編みを模様のラインに平行に折って立ち上げる場合の編み方でした。では、模様ラインに対して垂直に立ち上げるとどうなるでしょうか。
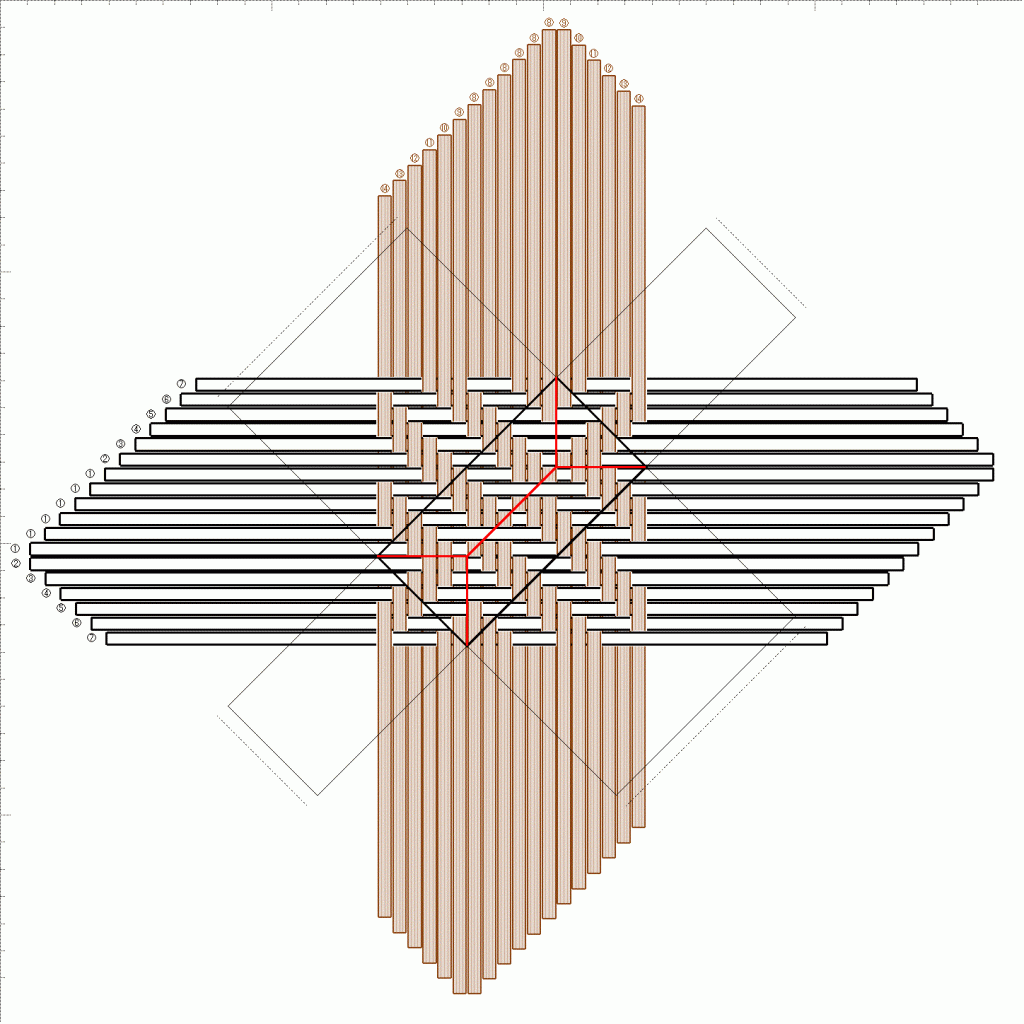
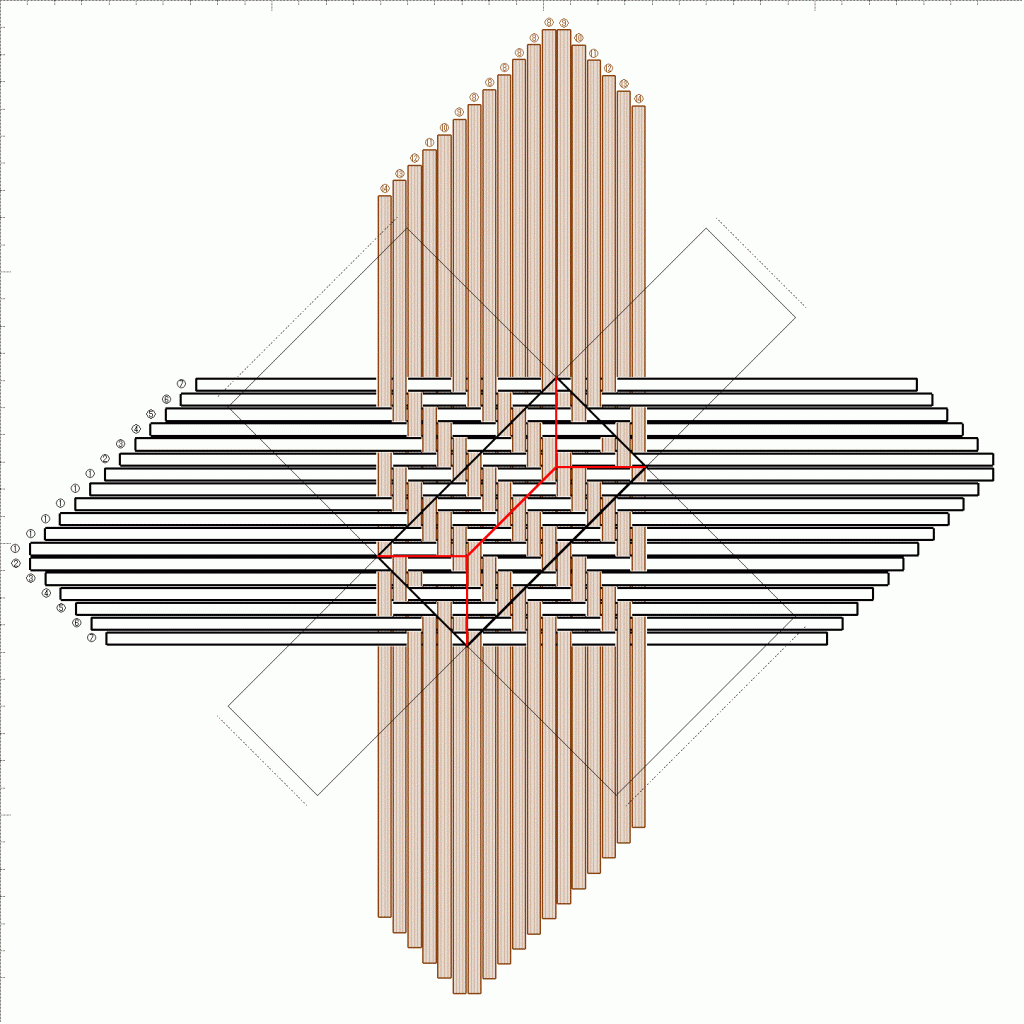
3つ飛び網代編み模様に対する立ち上げ位置は、次のいずれかになります。
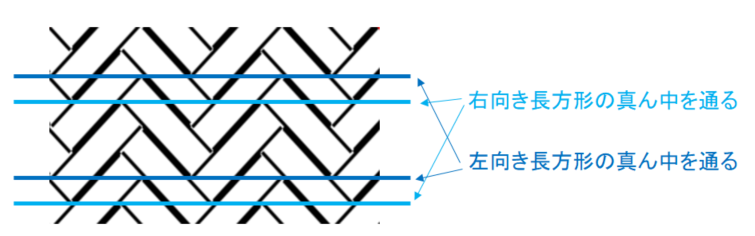
ラインに沿ったタイプでは、立ち上げ線は上の四角・下の四角・中の四角のいずれかひとつ、すべて同じ位置を通っていました。でも、こちらのタイプは、上の四角・下の四角・中の四角、全種を順に通っていきますから、上中下では区別できません。中の四角を通る時、長方形がどちらを向いているか、で識別することにしましょう。
立ち上げ線を水平に置いた時の、2パターンは次のようになります。
図の左を「左向き長方形」、右を「右向き長方形」とします。
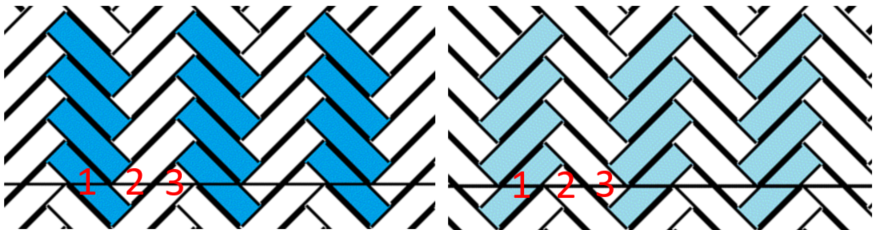 左向き長方形と、右向き長方形
左向き長方形と、右向き長方形
底の四角の位置に、1・2・3の数字を振っているように、3点の繰り返し模様です。ひも上下のデータ的には、上・下・下、もしくは下・上・上の 1-2 の繰り返しで、上下は、側面の角度が90度変わるごとに入れ替わります。1-2 のうち1が「左向き長方形」もしくは「右向き長方形」を通る方です。
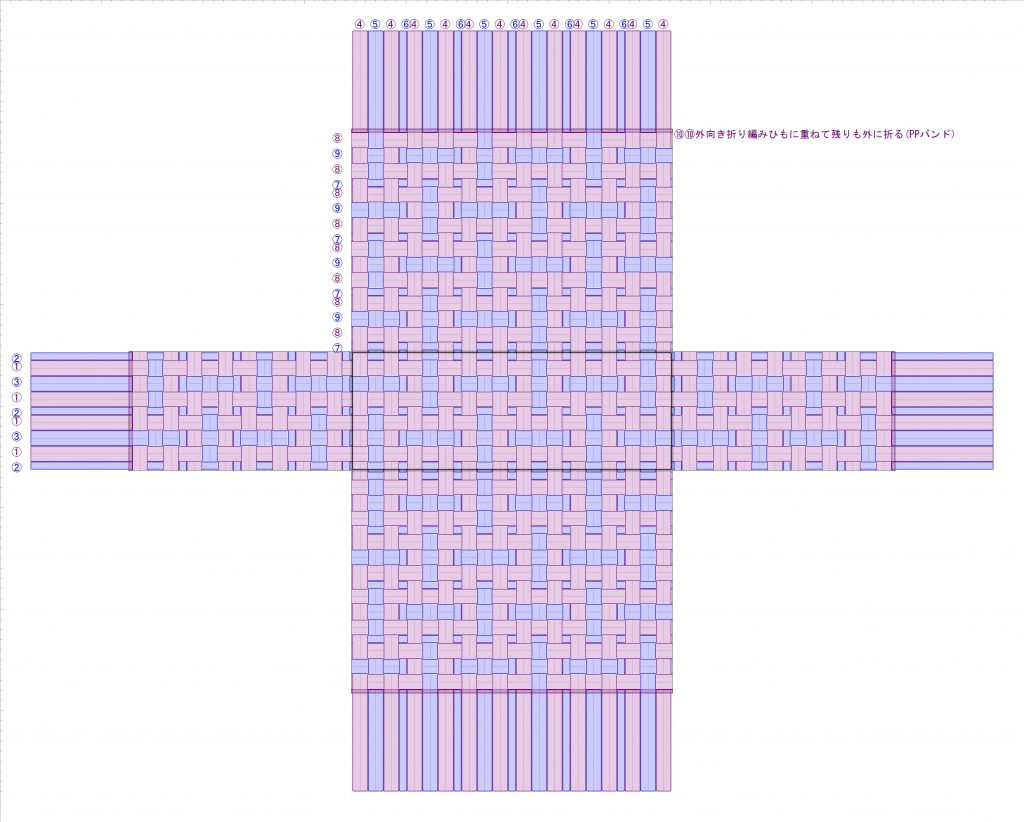
ラインに沿って立ち上げるタイプでは、側面の網代編みラインがつながるように、編み目を作りました。こちらのタイプも、まず各側面が底に対して垂直な網代編みラインになっているという前提で、同様にそのラインがつながるようにするには、
- (縦の四角数+横の四角数) が、3の倍数であること
- 底の周の4辺とも、同じ「左向き長方形」もしくは「右向き長方形」であること
- 底の角、即ちある側面から隣の側面に変わる箇所では、角の両側が上図の1・2・3の連続的な繰り返しになっていること
でしょうか。具体例を作ってみました。
つながらない例
側面によって「左向き長方形」と「右向き長方形」が異なっています。
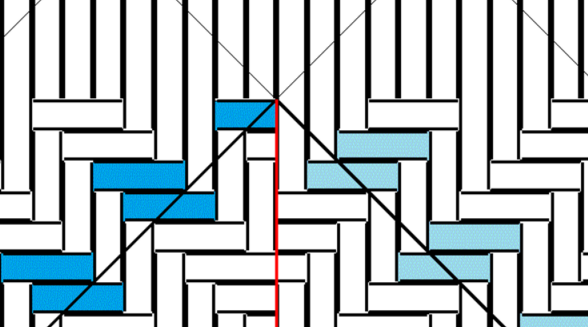 つながらない例
つながらない例
全て「右向き長方形」ですが、左の側面から右の側面にかけて、1・2・3になっていません。余分があります。
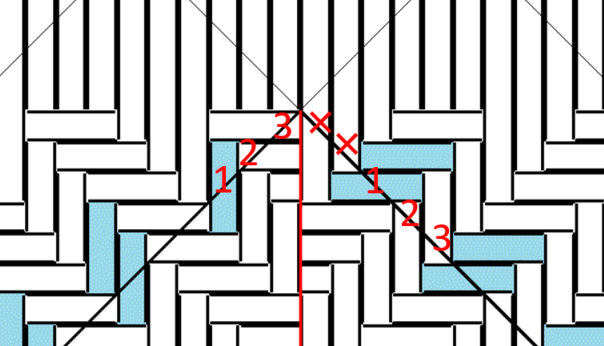 つながらない例
つながらない例
左の側面から右の側面にかけて、1・2・3になっていません。不足があります。
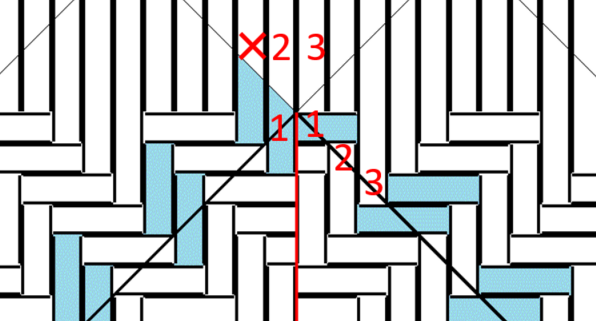 つながらない例
つながらない例
つながる例
全て「右向き長方形」で、底の上の角が左の側面から1・2、右の側面に回って3・1・2..と連続しています。
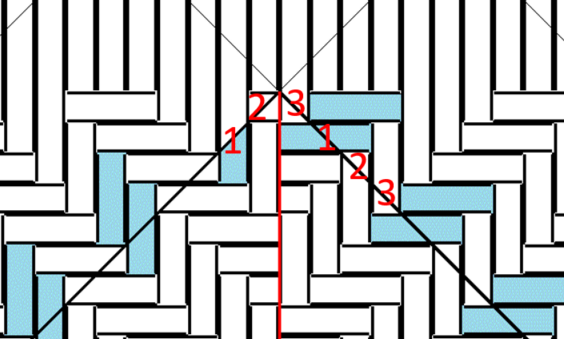 つながる例
つながる例
全て「右向き長方形」で、底の上の角が左の側面から1、右の側面に回って2・3..と連続しています。
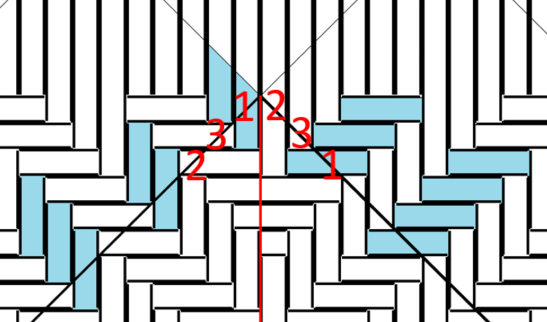 つながる例
つながる例
側面の辺
つながる例として2パターンを作ってみました。「右向き長方形」ではなく「左向き長方形」であったり、2番目の例「2・3・1/2・3・1」が「1・2・3/1・2・3」であったり、といろいろありそうです。
でも、対称性を考えると、上の2パターンに大別できるのではないでしょうか。
そして、この2パターンは、立ち上げた側面の形状が異なります。
- 立ち上げてできる側面、その位置に来る長方形の位置が、真ん中
- 立ち上げてできる側面、その位置に来る長方形の位置が、端(右端もしくは左端)
底の角が、立ち上げてできる側面の辺になります。並べてみました。
1.側面が長方形の3つの四角のうち、真ん中になるパターン。
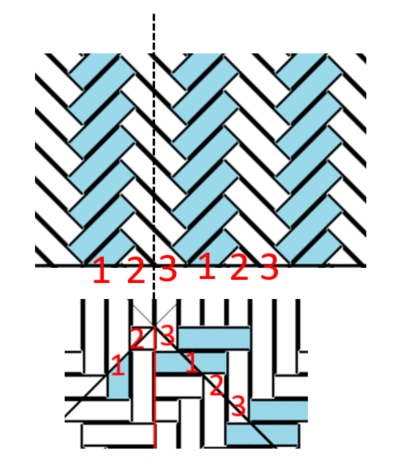 側面が中の四角
側面が中の四角
2.側面が長方形の3つの四角のうち、いずれかの端(真ん中以外)になるパターン。
 側面が端の四角
側面が端の四角
模様ラインに平行に立ち上げる場合は、立ち上げ位置は、上の四角・中の四角・下の四角でした。90度回転して、この3種が側面に来ている状態ですので、左の四角・中の四角・右の四角になるわけですが、右と左に関しては交換可能としてまとめて「端の四角」、そして残る「中の四角」ということになります。
さて、ここまで、側面をつなげるために、底はどうあるべきかを見てきました。ではこのあるべき状態に対して、長桝網代編みや四方網代編みのような決まった編み方というのはあるのでしょうか。そもそも、この編み方に、名前はついているのでしょうか。
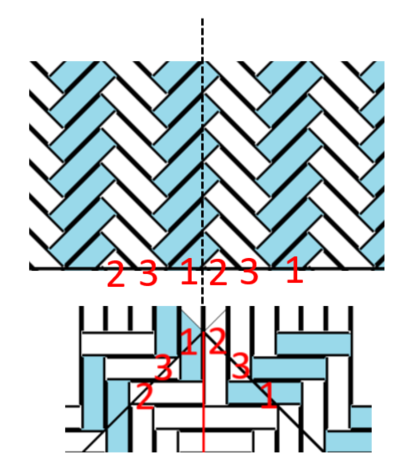
以前、このパターンのかごを作ったことがあります。「へリンボーン編み」という名前がついていました。底がどう作られていたか、改めて見てみましょう。