立ち上げ可能な繰り返し模様として、長桝網代の正方形パターンも試してみました。これも「中の四角」の位置です。
四角数6×6をベースとして、かごを作ってみました。中が3つ飛びの長方形で、できるだけ小さいサイズです。

底から見たところ。

条件については
| 1.~3 基本的な条件 | OK | |
| 4. 連続的 | △〇 | 一方は縦・一方は横ですが、高さ位置で揃うので |
| 5. 編みやすさ | 〇 | 長桝の1,3,5ベース |
| 6. 美しさ | 〇 | 模様らしくなってきましたが、単位が大きくなったからかも |
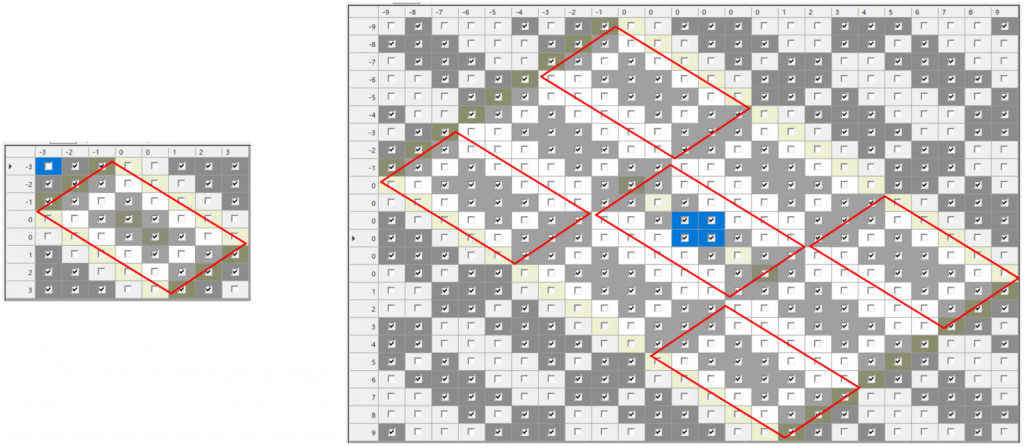
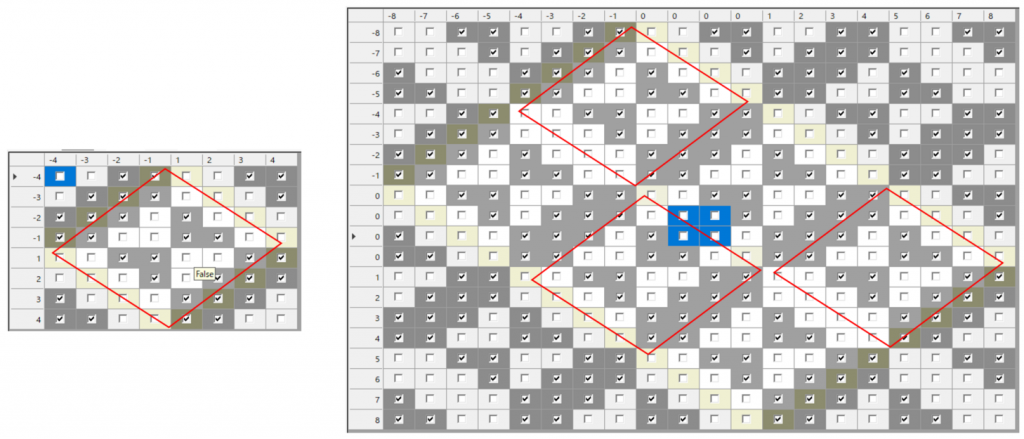
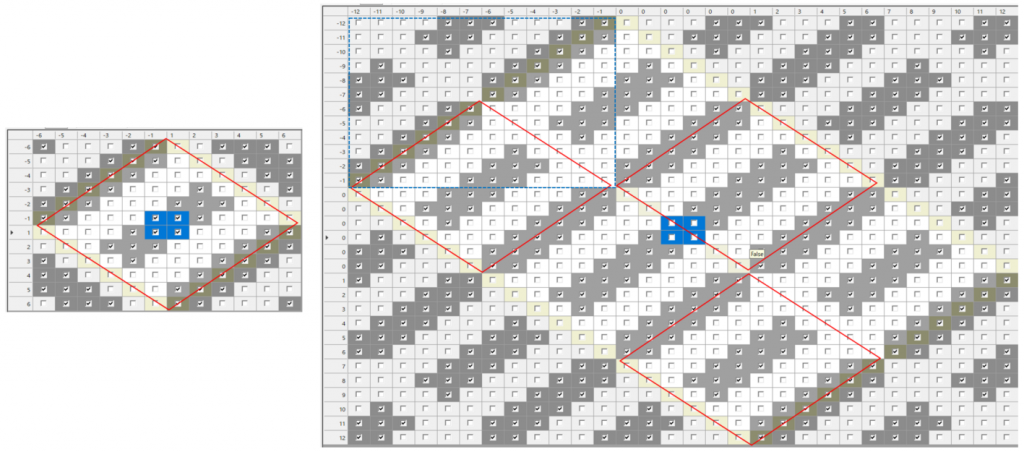
左側が、ベースとした四角数6×6の底の図です。右側は、それを2単位×3単位とした、四角数12×18の底の図。薄い黄緑のセルが底の辺で、繰り返しの1単位は、下図の赤枠内の菱形です。繰り返しの1単位は、右側の図の青点線部分の12×12です。
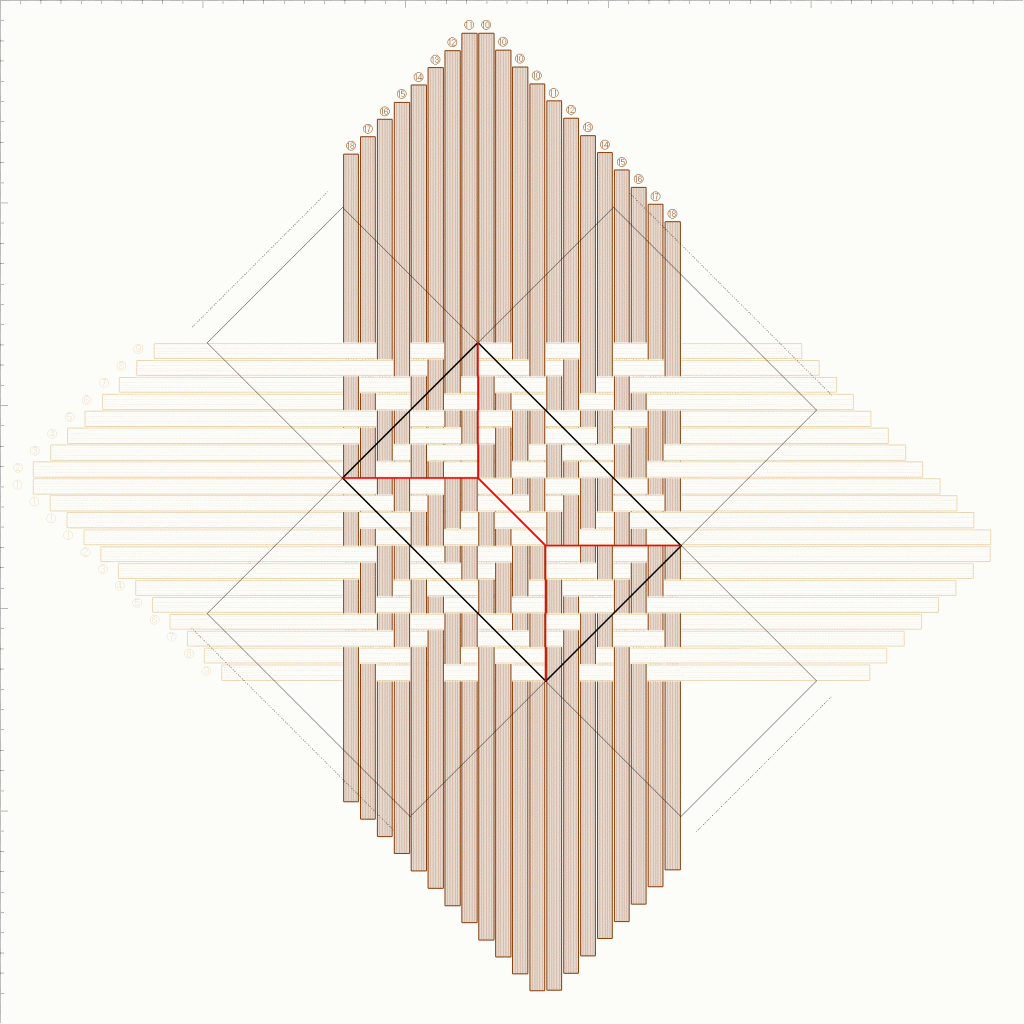
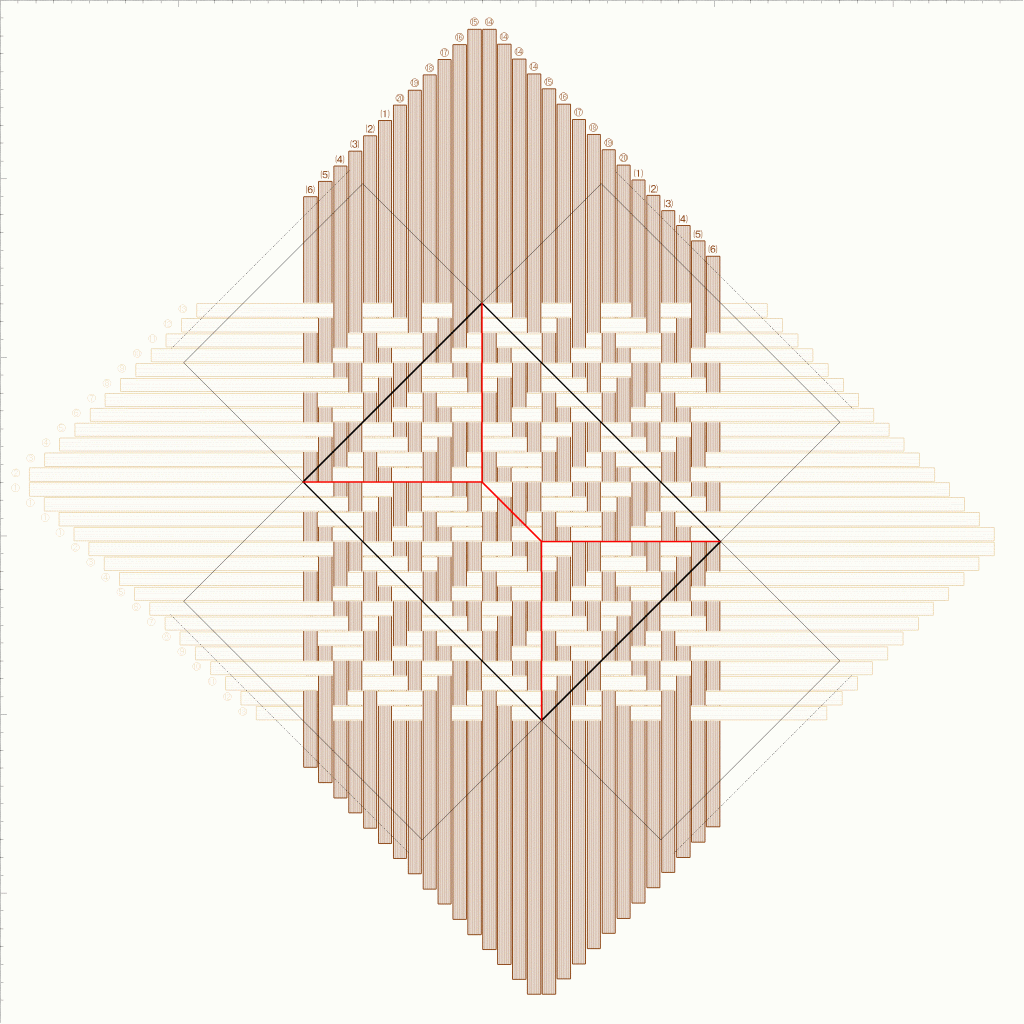
これを編み図にしたのがこちら。わかりやすいよう、縦ひもと横ひもの色を変えています。写真は、これを作ってみたものです。

データです。[ひも上下]には12×12の1単位が入っています。