いろいろな網代編みを集めてきましたが、いまのところ、(竹細工の)伝統的な模様の中には「斜め網代編み」という名前はありませんでした。たぶんこれは、クラフトバンド/紙バンドの用語なのでしょう。「斜め網代編み」という「模様」というより、「斜めに立ち上げる」という製法であり構造の総称として使われているようです。
竹細工の場合は「斜め」がデフォルトであり、わざわざ「斜め」をつける必要がないということなのでしょう。斜めではなく縦横に平行に立ち上げるのは、クラフトバンド/紙バンドでは普通です。でも、側面には底とは別の編みひもが必要であり、各段をボンドで貼り付けて輪にしたり、連続した長いひもを編んだりします。竹細工ではこちらの方が難しい。底からそのままつながる方が自然なわけです。
編み方との関係をチャートにしてみました。
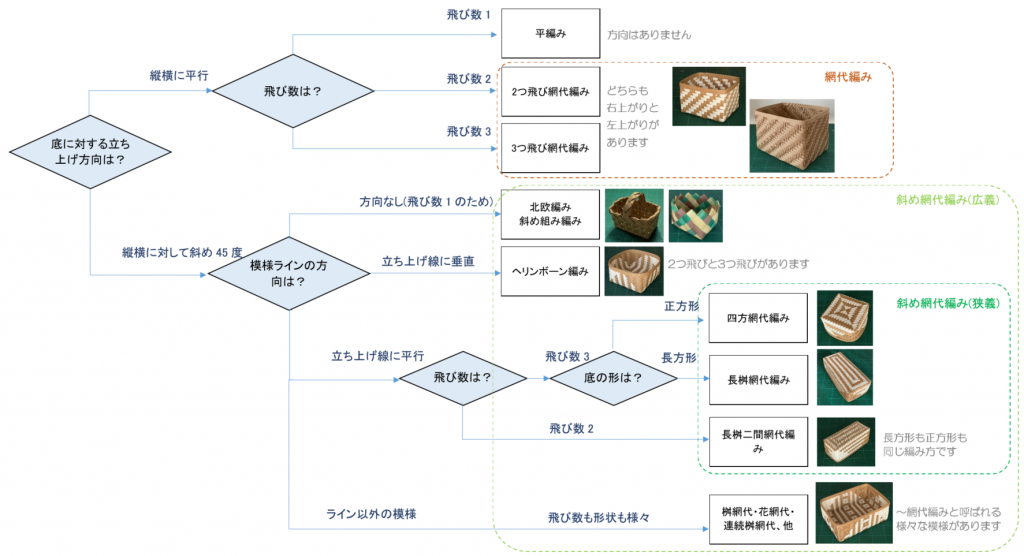 斜め網代編みの位置づけ
斜め網代編みの位置づけ
「斜め網代編み」としては、狭義では、斜め45度に立ち上げるタイプのうち、模様ラインが底と平行になっているもの。竹細工では、四方網代編み・長桝網代編み・長桝二間網代編みが相当しますが、クラフトバンド/紙バンドでは3つ飛びの斜め網代編みであっても、長桝二間網代編み風に作られるケースが多いようです。
広義では、模様ラインが底と垂直のものや、1×1を斜め45度に立ち上げるタイプも含まれるようです。
更には、模様網代が含まれるタイプも。ただ、模様が入る場合、「斜め網代編み」のカテゴリーに入るとは思いますが、できたかごは「~~模様のかご」と呼ばれるでしょう。ということは、構造の総称としてではなく「斜め網代編みのかご」という名前で呼ばれるとしたら、基本の網代編みで作られているということになるのでしょう。
ところで、ここまで出てきた編み方のポイントは、側面のために底をどう作るか、でした。立ち上げた時に・4つの側面が・同じ方向に揃った網代編みになるように、底でちょっと頑張る、といったらいいでしょうか。
その「揃った網代編み」は、シンプルな2つ飛びや3つ飛びの想定です。でも、網代編みには模様がたくさんあります。模様が入るとどうなるのでしょう。
長桝(二間)網代編み・四方網代編み・へリンボーン編みによって、側面の網代編みの方向が揃えられていたら、側面に繰り返し模様を入れるのはそう難しいことではないと思います。周全体の本数を模様の倍数にするとか、一部に入れるなら配置を合わせるなどの調整は必要にしても。
では、「側面のための配慮」などせずに、模様を優先して底を作る。それを立ち上げるとどうなるのでしょうか。やってみましょう。


















