2つ飛び網代編みの模様ラインが縦になるパターンで、小さいかごを作ってみました。
条件によれば、縦の四角数・横の四角数は、ともにどんな数でもよい、ということで した。偶数ではできて当然でしょうから、縦ひも+横ひもの数が奇数になるよう、四角数11 × 10、ひも数21本にしてみました。
まず側面を縦方向に2つ飛び網代編みで作り、角の位置を条件に合うように合わせ、底をできるだけ自然な模様にする、という手順です。
底です。3つ飛びの「端の四角」のような模様になりました。
編み図です。
データです。
では、3つ飛びと同様に、2つ飛びについても、模様ラインに対して垂直に立ち上げる場合はどうでしょうか。
立ち上げ位置は、次のいずれかになります。
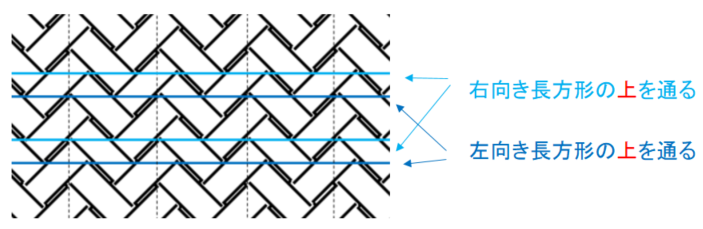
2つ飛びの場合は、上の四角と下の四角の2つしかないので、上の四角の方で識別することにします。左右・上下を通るラインが上の四角になっている方に注目し、それが右向きか、左向きか、を見るということです。
立ち上げ線を水平に置いた時の2パターンは次のようになります。
図の左を「左向き長方形」、右を「右向き長方形」とします。
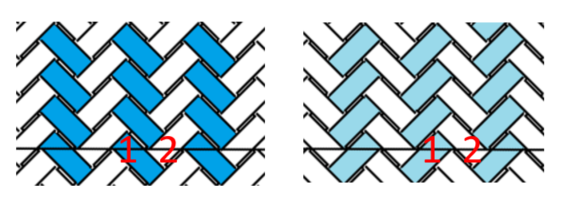
底の四角の位置に、1・2の数字を振っているように、2点の繰り返し模様です。ひも上下のデータ的には、上・下もしくは下・上の 1-2 の繰り返しで、上下は、側面の角度が90度変わるごとに入れ替わります。
ラインに沿って立ち上げるタイプでは、側面の網代編みラインがつながるように、編み目を作りました。こちらのタイプも、まず各側面が底に対して垂直な網代編みラインになっているという前提で、同様にそのラインがつながる条件は、
なお、底の周の四角数については「(縦の四角数+横の四角数)×2」であり必ず偶数になりますので、「2の倍数である」という条件は、どんな数であっても成立します。
これも、具体例を作ってみましょう。
側面によって「左向き長方形」と「右向き長方形」が異なっています。
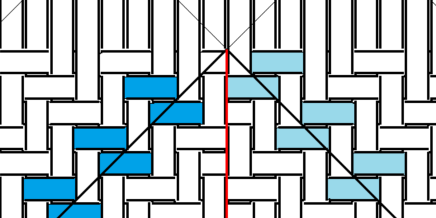
全て「右向き長方形」ですが、左の側面から右の側面にかけて、1・2・1・2になっていません。余分があります。
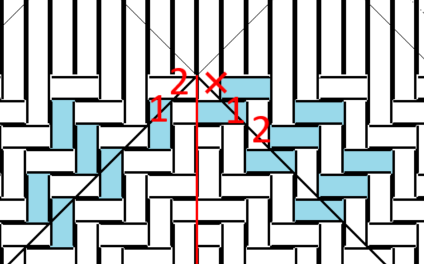
左の側面から右の側面にかけて、1・2・1・2になっていません。不足があります。
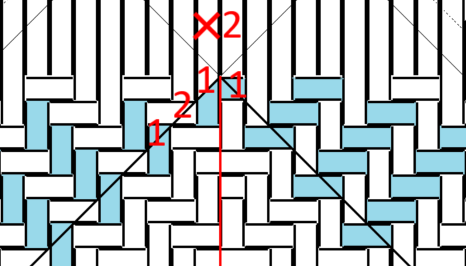
全て「右向き長方形」で、底の上の角が左の側面から2、右の側面に回って1・2..と連続しています。
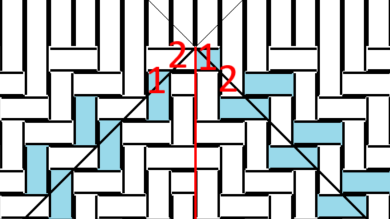
全て「右向き長方形」で、底の上の角が左の側面から1、右の側面に回って2..と連続しています。
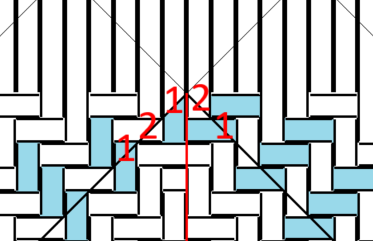
2つの例を載せましたが、要は角の両側に1と2です。3つ飛びのように側面の状態が変わるわけではなく、ともに端の四角位置で、実質同じと見て良いのではないでしょうか。
そして、編み方の名前は何でしょう？
3つ飛びは「ヘリンボーン編み」でしたが、こちらも同じ「ヘリンボーン編み」でよいのでしょうか？
立ち上げ位置の検討で、３つ飛びを模様ラインに平行に折る場合、折り位置は「上の四角」「中の四角」「下の四角」のいずれかでした。2つ飛びではどうでしょう。
四角が2つでできた長方形ですから「上の四角」/「下の四角」、これと「右向き」/「左向き」を組み合わせると
となります。
3つ飛びの時と同様、左右については交換可能ということで、これを「上の四角」と「下の四角」として識別することにしましょう。
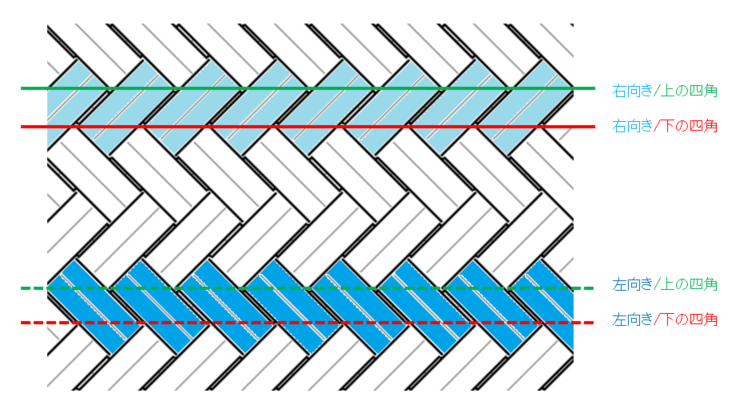
次は「角(かど)にかからない中央部分」を見てみます。3つ飛びの時と同様、模様ラインと平行になるように長方形の底を立ち上げた場合、長辺側つまり模様ラインと平行になる部分の中心の飛び数は、1もしくは3になります。
何故なら、全体が正方形ですから、斜めの中心線は四角の対角線を通ります。でも、四角2個の長方形(2つ飛び網代編み)には、対角線を通る中心線は存在しません。従って、中心部分が2つ飛びになることはあり得ない。また、中央ラインは四角の間には来ないのですから、4で割った余りから0と2を除外すると、1もしくは3になるのです。
下図のいずれかです。
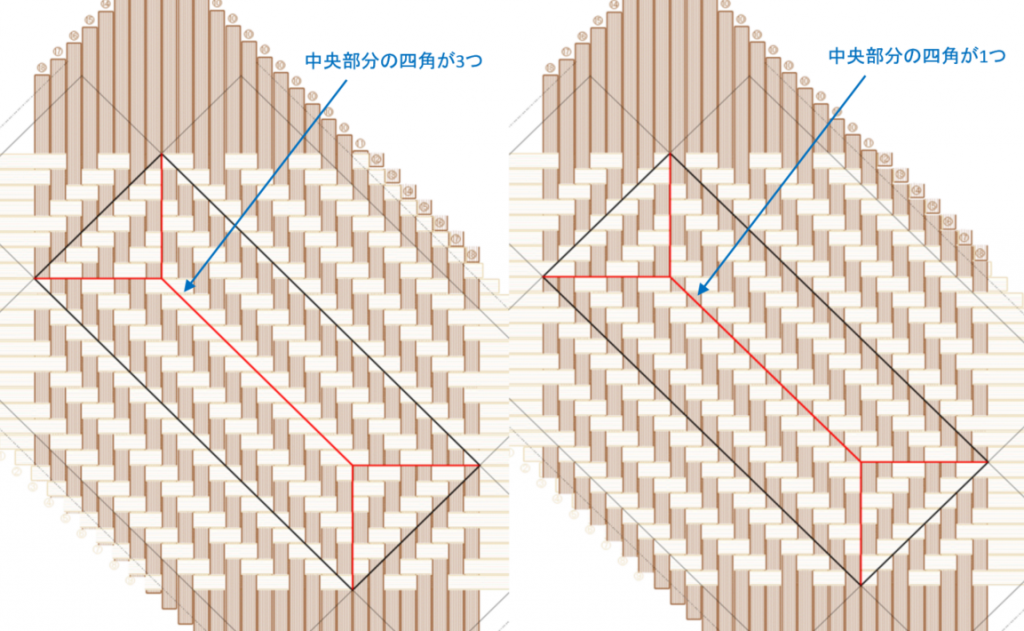
「八女市伝統工芸館」の「52 交色長桝二間網代」では、中央部分は3つ飛びになっていました。
2つ飛びの長桝網代については、文献
『図説 竹工芸 : 竹から工芸品まで』佐藤庄五郎、共立出版、1974
223ページ、図11.3 ますあじろの変化と四方あじろ・長ますあじろの一連の図の中に「(f)長ますあじろ(交色)」として掲載されています。こちらも、中央部分は3つ飛びになっています。ですので、竹編みの場合、中央部分を3にするのが正しい長桝二間網代と言えそうです。
かつて、斜め網代編みの底の組み方を検討した時、とりあえずのルールとして、
「上の四角」で立ち上げることを優先する。その結果、中央部分は1もしくは3になる。
としました。正しい長桝二間網代の場合は、そうではなく、
中央部分が3になることを優先する。その結果、立ち上げ位置は「上の四角」もしくは「下の四角」になる。
というルールだったのでした。
「角(かど)の三角形部分」はどうでしょう。3つ飛びの長桝網代編みでは長方形につながっていましたが、2つ飛びの場合は、対角線で反転した模様になっています。「八女市伝統工芸館」の「52 交色長桝二間網代」も『図説 竹工芸 : 竹から工芸品まで』ともにです。
短辺側の四角数を同じとし、長辺側の数を変えた図を並べてみました。短辺側、下図では左上と右下の直角二等辺三角形部分は、全て同じ編み方です。3つ飛びの時は短辺側は仮の絵でしたが、2つ飛びの場合は反転状態そのままの絵ですから、角(かど)の三角形部分については、短辺の四角数が同じであれば、長辺側の数によらず編み方は同じ、ということになります。
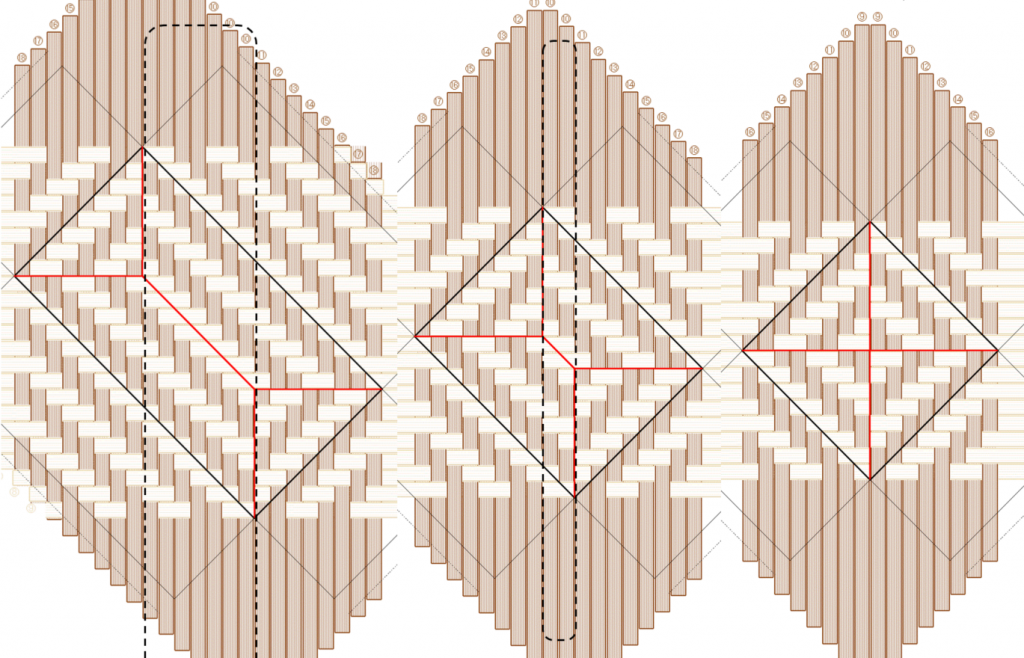
そして、短辺と長辺が同じになる、つまり横の四角数=縦の四角数・正方形になると、四方網代(風)になるのです。
「長桝網代編みを正方形にしても四方網代編みにはならない・別の編み方である」というのが3つ飛びだったのですが、2つ飛びの場合は
長桝二間網代編みを正方形にすると四方網代編みになる・同じ編み方である
ということになるのです。何てことでしょう。。
ただしこれは、上図の一番右の編み方を何と呼ぶか、「長桝二間網代編み」なのか「四方網代編み」なのか、にかかってきます。見た感じ「長」より「四方」の方が自然に思えますが「四方二間網代編み」という言葉はあるのでしょうか。
そして、CraftBandSquare45による底の編み図の生成方法。3つ飛びの場合は、違う2種類の編み方、設定パターンも各3点あったため、早見表が便利でした。でも2つ飛びの場合は、編み方はひとつしかないし、設定パターンも次の2つしかありません。
1.の値が既定値になっていますので、そのままでも1/2の確率で生成できます。だめなら、2.の値に変えればよいだけ、なのです。
| 名称 | 長桝二間 網代 編み 長桝 網代 編み |
| 名称(読み) | ながますふたま あじろ あみ ながます あじろ あみ |
| 模様タイプ | 中心2点間は3つ飛び、各領域2つ飛び |
| 単位 | |
| バンド幅 | |
| 色 | |
| 飛び数 | 1,2,3 |
| 対称性 | 半回転 |
| 備考 |
「八女市伝統工芸館」の「竹編組見本」から「52 交色長桝二間網代」でボックスを作ってみました。
「竹編組見本」は、平らに編まれていますが、長桝網代編みと同様に長方形に立ち上げました。「長桝二間網代」という名前の通り、二間網代編みベースです。側面の二間網代編みがつながるように作りました。
底です。3本飛びの長桝網代編みとはちょっと異なる模様です。長方形がつながっていません。
そして、3本飛びと比べると二重に編みにくいです。
編み図です。
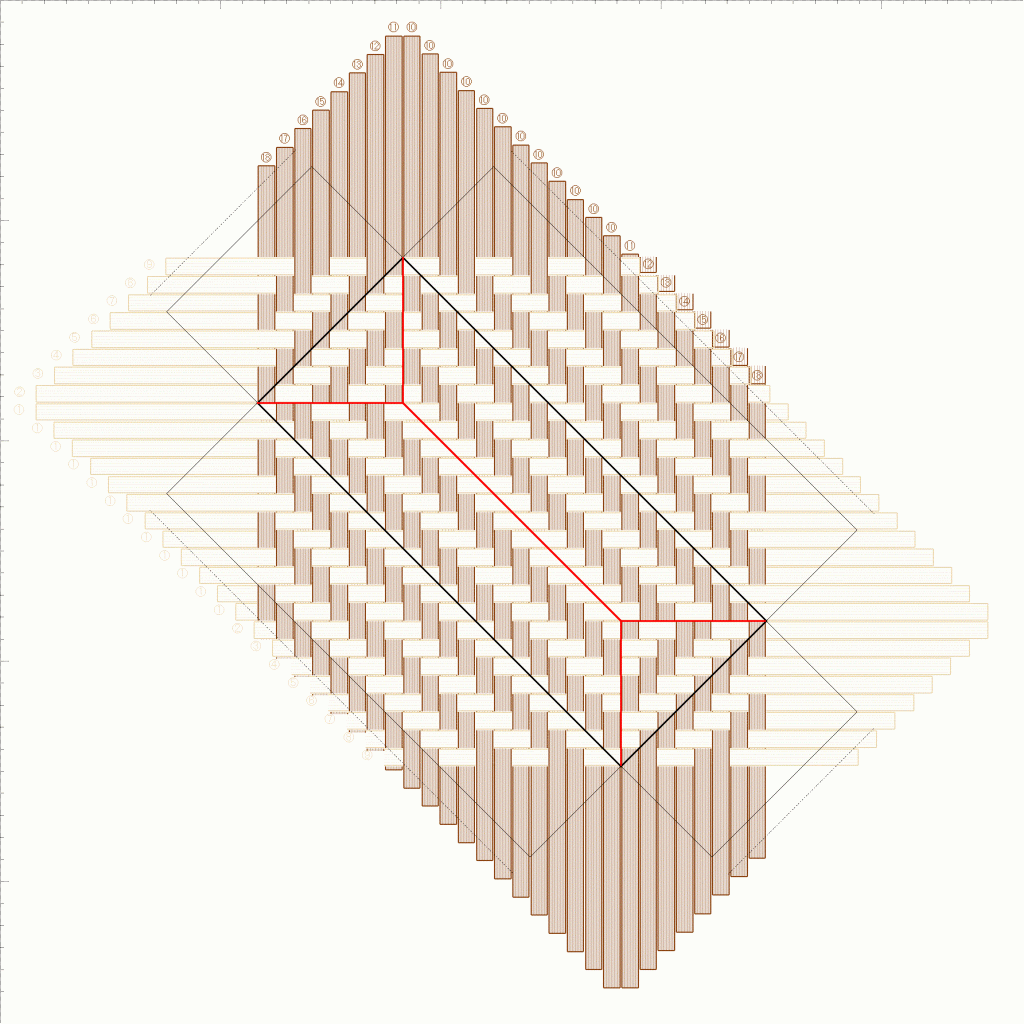
データです。
| 名称 | 二間 網代 編み 2つ飛び 網代 編み 2本飛び 網代 編み 2本飛ばし 網代 編み 二目 網代 編み |
| 名称(読み) | ふたま あじろ あみ ふたつとび あじろ あみ にほんとび あじろ あみ にほんとばし あじろ あみ にもく あじろ あみ |
| 模様タイプ | 単位の繰り返し |
| 単位 | 4 × 4 |
| バンド幅 | |
| 色 | |
| 飛び数 | 2 |
| 対称性 | 半回転 |
| 備考 | 右上がり、左上がり |
「八女市伝統工芸館」の「竹編組見本」から「45 二間網代」で小さいボックスを作ってみました。
実はこの「二間」の読み方がわからなかったのです。「にけん」「にかん」「にま」「にげん」「ふたま」(読み方自体は他にもあるようです)… 竹細工をされている方にお聞きして「ふたま」としましたが、良かったでしょうか。
CraftBandSquare のデータです。側面は、設定データにある「4×4-22-網代編み2つ飛び」そのままです。底はサイズに合わせ、側面からの2つ飛びがそのままつながるよう、少し編集してみました。
データです。