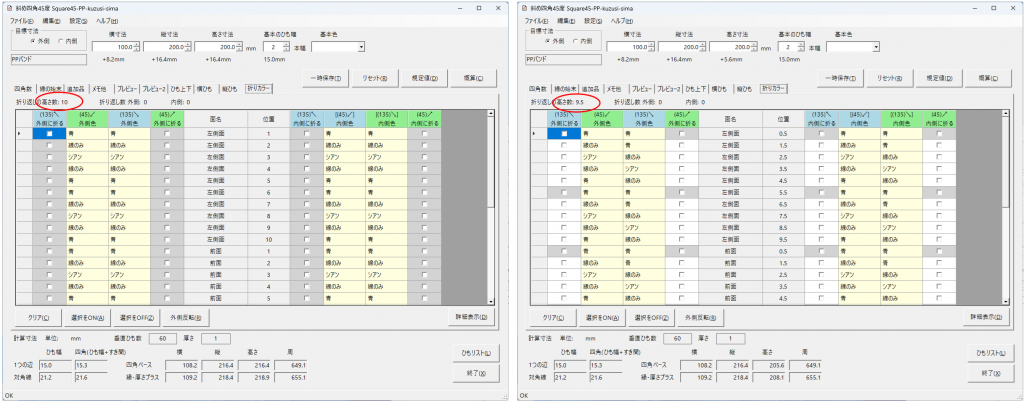
折りカラー編みでは、側面で折り返したバンドを底まで編み重ねますが、底の中はどこまで重ねたらよいのでしょう。今まで、各辺からのバンドは、とりあえず底の中央線までとしていましたが、改めて、位置を変えて比べてみました。

縦横の四角数は5と6、最初の配置や折り返しは同じで、底の中でどこまで重ねるか、を変えた3種、格子(ドット)模様です。

左から、A:底の辺、B:中間位置、C:底の中央線、まで重ねたときのパターンです。長辺側が重なっている例となります。

同様に、左から、A:底の辺、B:中間位置、C:底の中央線、まで重ねたときのパターンです。短辺側が重なっている例となります。

まず、それぞれの数を数えてみました。辺にかかる部分を除いてカウントした値に、辺上のカウントをカッコ付きで加えています。

同じ色が連続する四角数の最大

C:底の中央線では最大2で、大きく連続することはない。辺に近づくほど連続した領域が大きくなっていきます。

同色領域数	A:底の辺	B:中間位置	C:底の中央線
外側・黒の最大数	13	9	2
外側・赤の最大数	1	2	2
内側・黒の最大数	11	7	2
内側・赤の最大数	1	2	2

バンドごと、同色2点が並ぶ数

C:底の中央線まで重ねたパターンが、２個並び数が一番少なくなっています。２個並び数が少ないほど、格子模様に近いと言えるでしょう。

２個並び数	A:底の辺	B:中間位置	C:底の中央線
外側・横ひも・黒	12	10	6
外側・横ひも・赤	0	2	4
外側・縦ひも・黒	12	10	6
外側・縦ひも・赤	0	2	4
外側・２個並び数合計	24	24	10
内側・横ひも・黒	10	8	6
内側・横ひも・赤	0	2	4
内側・縦ひも・黒	10	8	6
内側・縦ひも・赤	0	2	4
内側・２個並び数合計	20	20	10

同じ色が並ばない、独立した四角の数

重なり位置が、中央から遠いほど、独立した四角の数が増えています。一番多いのは、A:底の辺のパターンです。独立した四角数が多いほど、格子模様に近いと言えるでしょう。

独立四角数	A:底の辺	B:中間位置	C:底の中央線
外側・黒の独立四角数	15 (+6)	5 (+14)	6 (+14)
外側・赤の独立四角数	24	18	13
外側の独立四角数	39 (+6)	23 (+14)	19 (+14)
内側・黒の独立四角数	16 (+8)	8 (+14)	6 (+14)
内側・赤の独立四角数	20	19	13
内側の独立四角数	36 (+8)	27 (+14)	19 (+14)

同じ色が連続する領域の数

同じ色が一続きになっている領域を1と数えます。最小の独立四角、最大の同色領域、いずれも1です。
A:底の辺が一番多く、次いでC:底の中央線、B:中間位置の順です。領域数が多いほど、格子模様に近いと言えるでしょう。

同色領域数	A:底の辺	B:中間位置	C:底の中央線
外側・黒の同色領域数	17 (+6)	7 (+18)	12 (+18)
外側・赤の同色領域数	24	22	21
外側の同色領域数	41 (+6)	29 (+18)	33 (+18)
内側・黒の同色領域数	18 (+8)	10 (+18)	12 (+18)
内側・赤の同色領域数	20	23	21
内側の同色領域数	38 (+8)	33 (+18)	33 (+18)

その他の指標

指標	A:底の辺	B:中間位置	C:底の中央線
バンドの使用量	◎　少ない	〇　少し多い	△　多い
底の丈夫さ	△　二重	〇　二重/四重	◎　四重
編む手間	◎　少ない	〇　少し多い	△　多い
切り替え位置	◎　わかりやすい	△　わかりにくい	〇　慣れればわかる

まとめ

比べてみると、どの点から見てもベスト、というパターンはありません。用途、サイズ、色、模様、素材、手間その他を総合的に勘案して、何を選ぶかでしょう。

なお、選択にあたっては、赤のバンドと黒のバンドは交換可能ですし、長辺側/短辺側は折り返し方向を変えれば入れ替えられます。また、A/B/C については内側と外側は同じである必要はなく、例えば外側はA:底の辺・内側はB:中間位置などとすることもできます。

縦横の四角数は5と6という、あくまで一例ではありますが、代表的なパターンとその傾向として、判断材料になればと思います。

データです。３点とも同じです。Ver1.9 からの .cbmesh ファイルですが、旧Verでもそのままドラッグすれば開けます。