折りカラー編みは、裏表のない、つまり両面とも同様に使えるバンドが前提です。
では、表裏がある、つまり片面しか使えないバンドだったらどうでしょう。
二色を使ったとしたら、同じ様な模様が作れるのでしょうか。
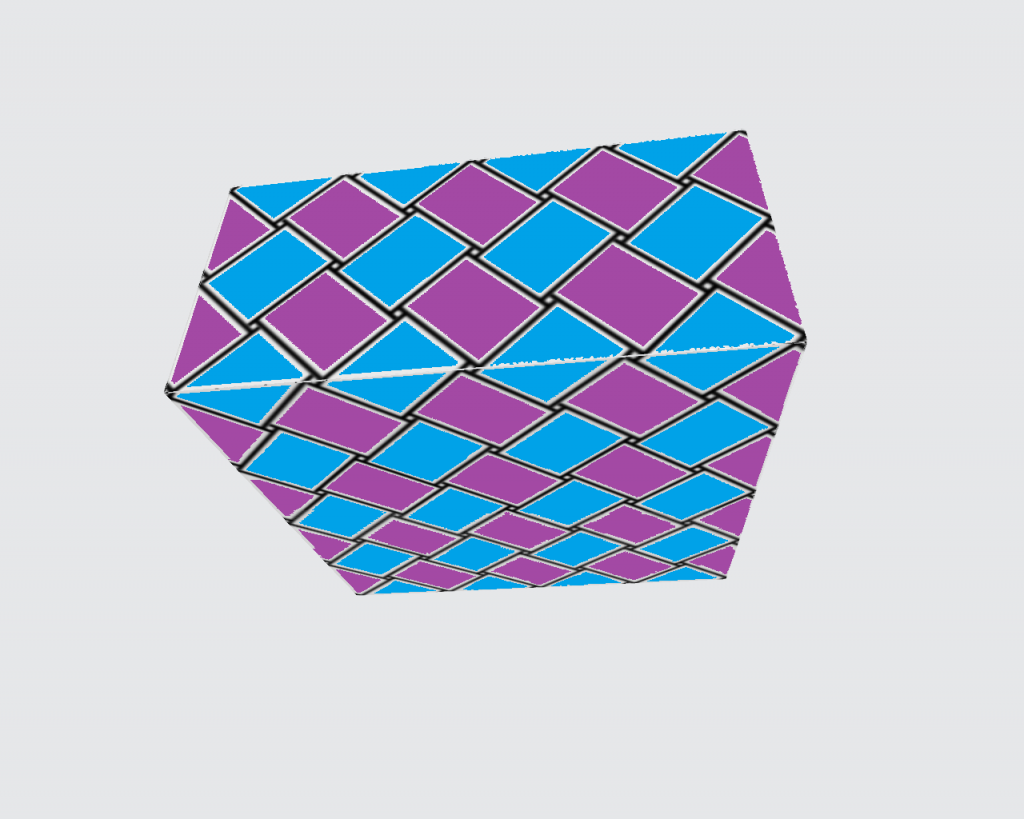
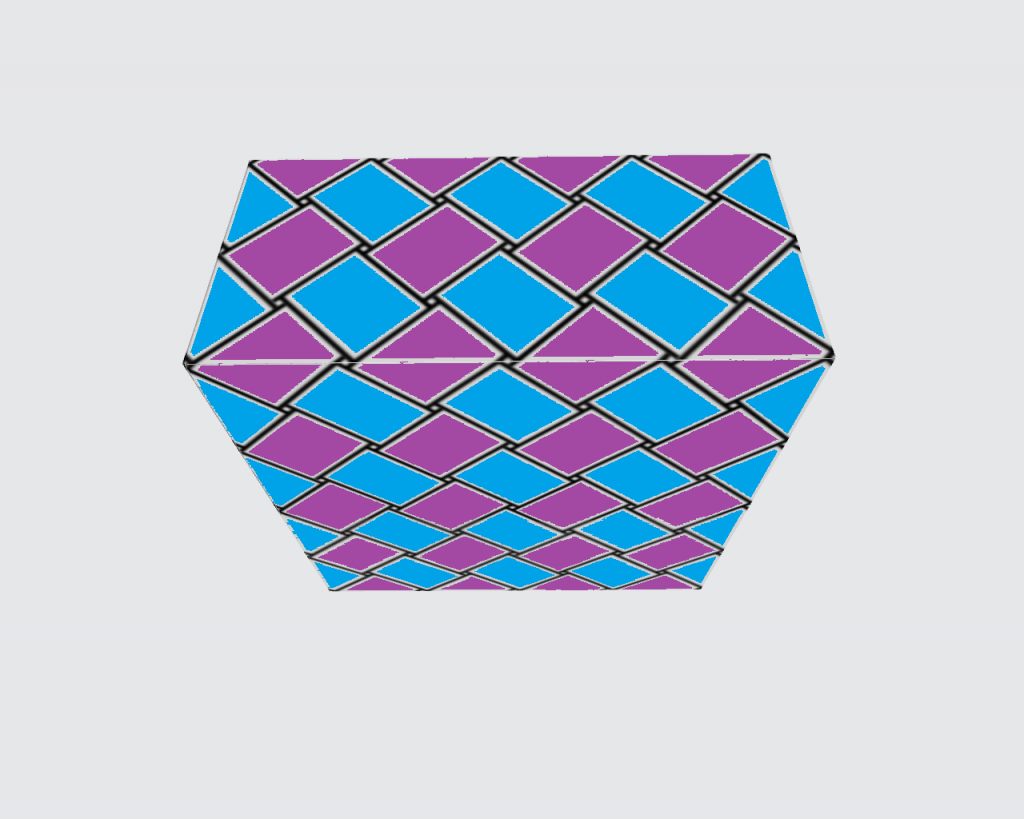
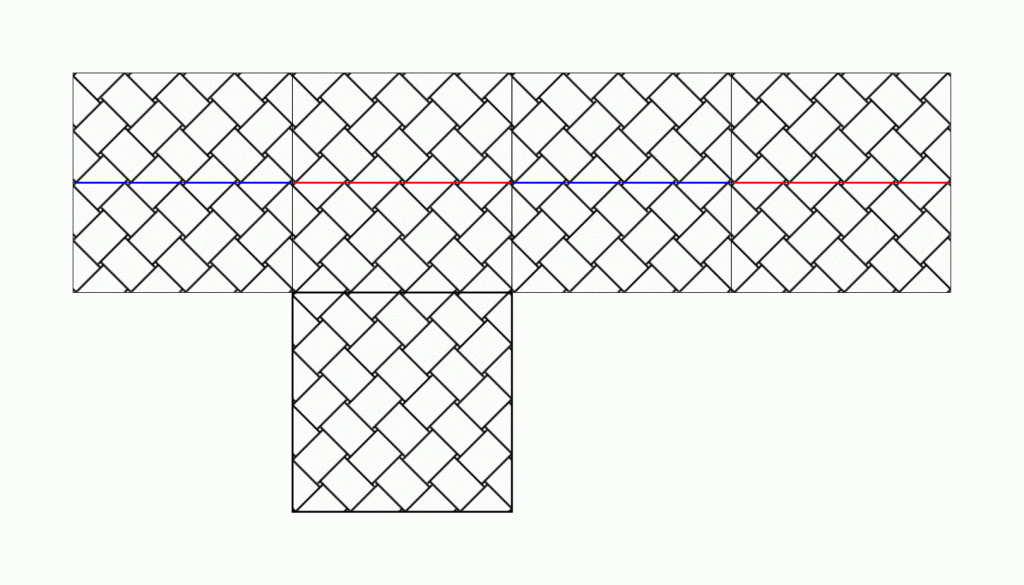
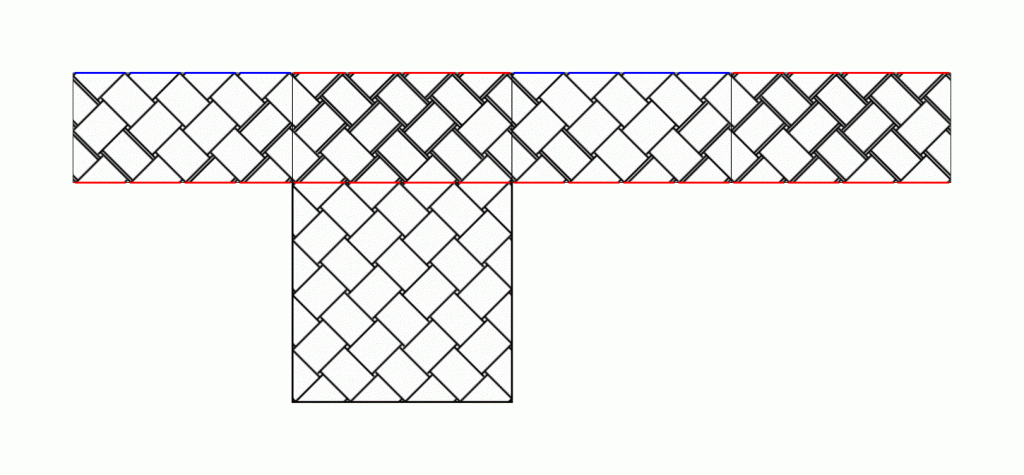
片面にだけストライプがあるPPバンドで試してみました。
底が正方形のライン模様のかごなら何とか。でも、ドット模様のような交色にするのは難しそうです。
実はこの試みは、紙バンドの先生から、折りカラー編みについて次のように尋ねられたことがきっかけでした。
白樺細工の編み方と同じですか？
白樺細工（ネーベルスロイド）は、外側も内側も表面が出るように編んでいくので、紙バンドのように、上側だけで始末せず全体的に２重に編んでいきます。
このサイトは2022年末からですから、まだ新参者もいいところです。私が始めた頃にはすでに、白樺細工そのものではなく、「北欧風編み」として、紙バンドやティムテープでの作り方が確立されていました。材料も豊富に揃っていましたし、私も斜め編みの一種としてしか認識していなかったのです。
先生のお話をきっかけに、あらためて白樺細工について調べてみました。
すると、白樺の樹皮は、外側は白く、内側は茶色でしっとりとした風合いをもち、かごにする際には、基本的に樹皮の内側だけを使うということが分かりました。
なるほど、さすが紙バンドの先生です。
長年のご経験と知識に裏打ちされた視点だと感じました。
折り返して重ねるという構造は、まさに折りカラー編みそのものです。
では、色についてはどうでしょうか。
テープ状に加工した樹皮を、二色使いできないだろうか、と考えてみました。
まずは、表皮の白と内側の茶色を、二色として扱えないかです。
しかし、これはなかなか難しそうです。
二色が交差する高さ位置で対角線に折ったとしても、下図・左のように、同じ色が重なるだけです。では、下図・右のように、一色が交差する高さ位置［※］で、セットではなくどちらかだけ折り返すのは？ でも、一本だけでは、内側と外側が分離してしまいます。
それならば別の方法として、内側が濃い茶色の樹皮と、薄い茶色の樹皮を選び、二色として扱うのはどうでしょうか。この場合、テープとして使う際には、その片面だけを使うことになります。
でも、折りカラー編みの交色は、どれか一本のバンドを辿ってみると、表側が表出している箇所と、裏側が表出している箇所の両方が組み合わさっています。そうなると「常に表側だけを見せる」という作り方自体が難しそうです。
結局のところ、この試作例の片面つまり裏表のあるバンドで作れたのは、既知のパターンをそのまま底まで折り返しただけのかごです。
ですから、このときに現れたライン(ストライプ)模様も、決して特別なものではありません。従来のやり方の延長で生まれる、ごく自然な模様です。
何百年と続く白樺細工の歴史の中で、誰が作っていても不思議ではない、その程度のものだと思います。
もし、それが実際には残されていないのだとしたら――
やはり白樺細工は、単色であるべきものなのかもしれません。
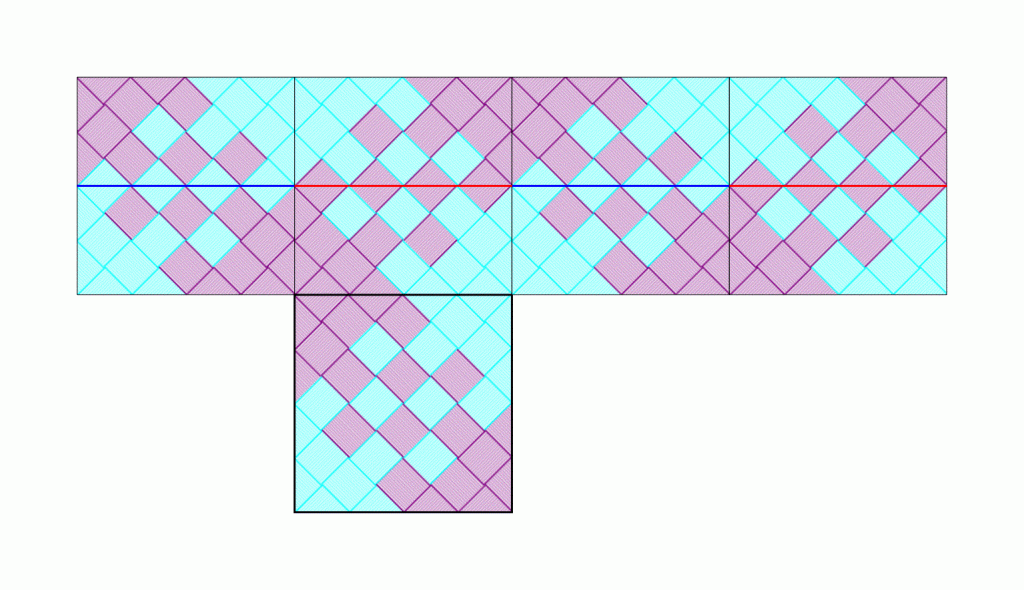
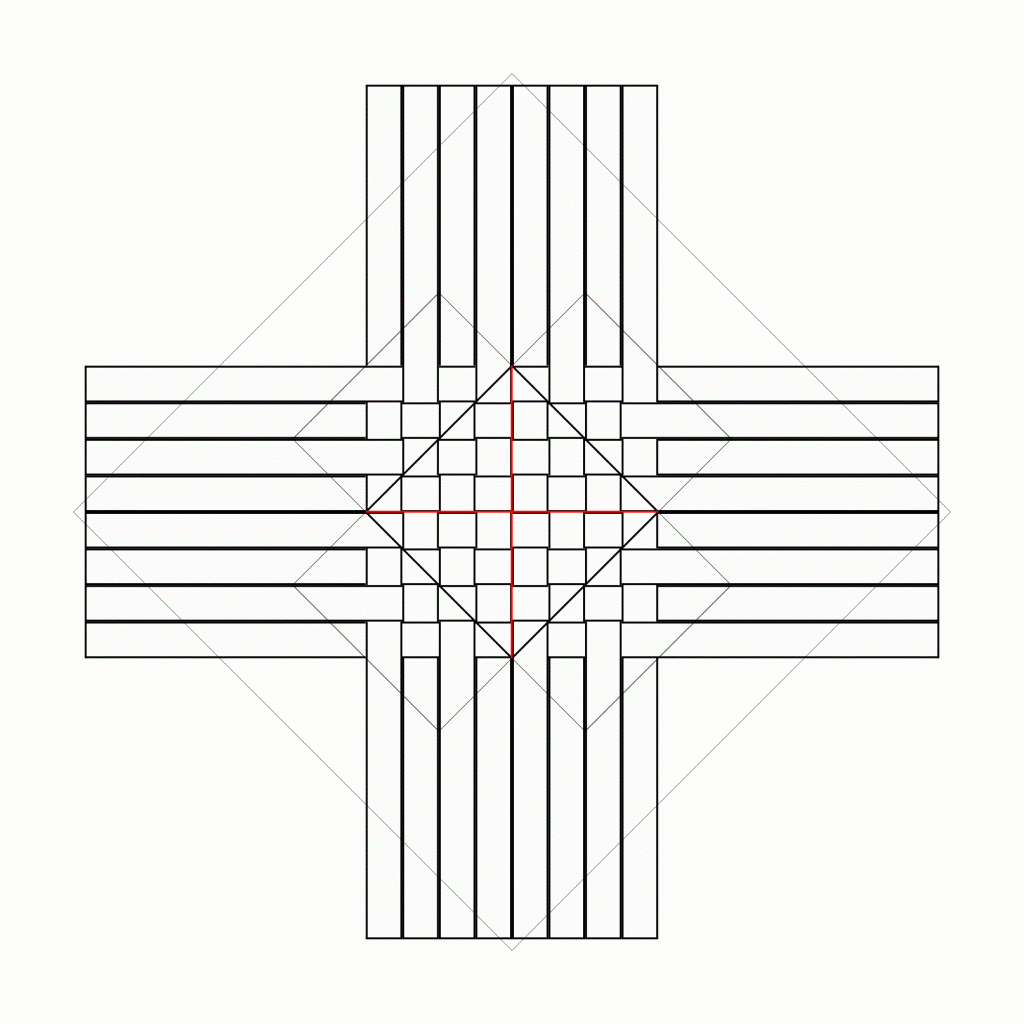
Square45のデータです。
「PPバンド(3本幅扱い)」に、赤ライン,青ラインを追加しましたので、設定ファイルもつけておきます。
