先に使った墨流しのひもですが、素材の墨流し模様がもうすこし広く見えるように作ったら、どうなるでしょう。2-1の網代模様で作ってみました。
和紙だけだとやわらかくなるので、12本幅の白の紙バンドを芯にして、開いた顔墨ひらりと和紙とを巻きました。硬い箱になりました。
底と内側です。
平編みではなく、2-1ベースのちょっとイレギュラーな網代編みです。型紙は使わず、完成した底編み図を見ながら、中心から外に組んでいったのですが、上下が混乱してしまいました。バンドを加えるごとに色パターンが変わってしまうからです。端から順に並べるなら簡単なのですが。
ということで、作る時には、こんな図を並べておくと便利です。Ver1.9.1 の機能(表示順画像生成)を使えば、ワンクリックでこの7枚が作れます。
そして、底を折って立ち上げた後は、以下の図を表示させ、実物と方向を合わせながら側面を編みました。その後、高さ3で折りカラー編みです。
データです。表示順番号も入っていますので、機能のテストにどうぞ。
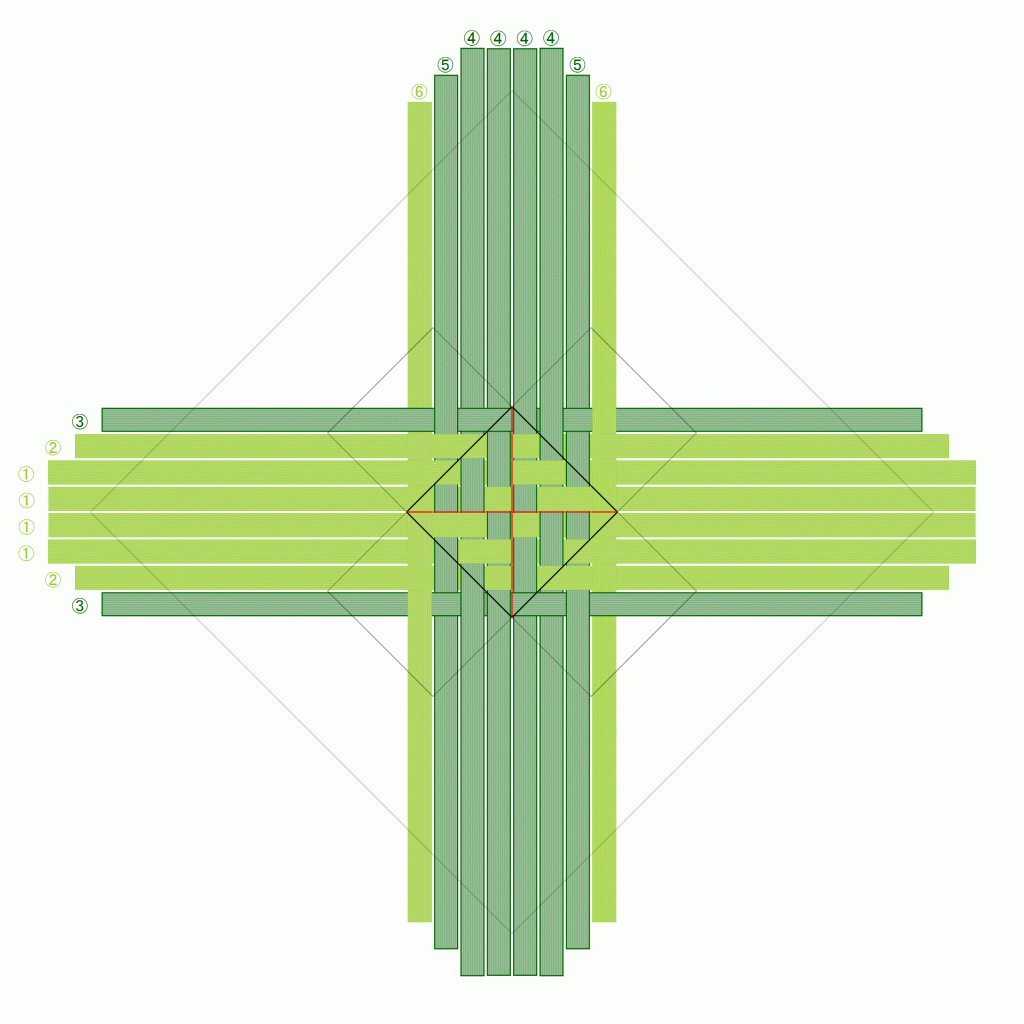
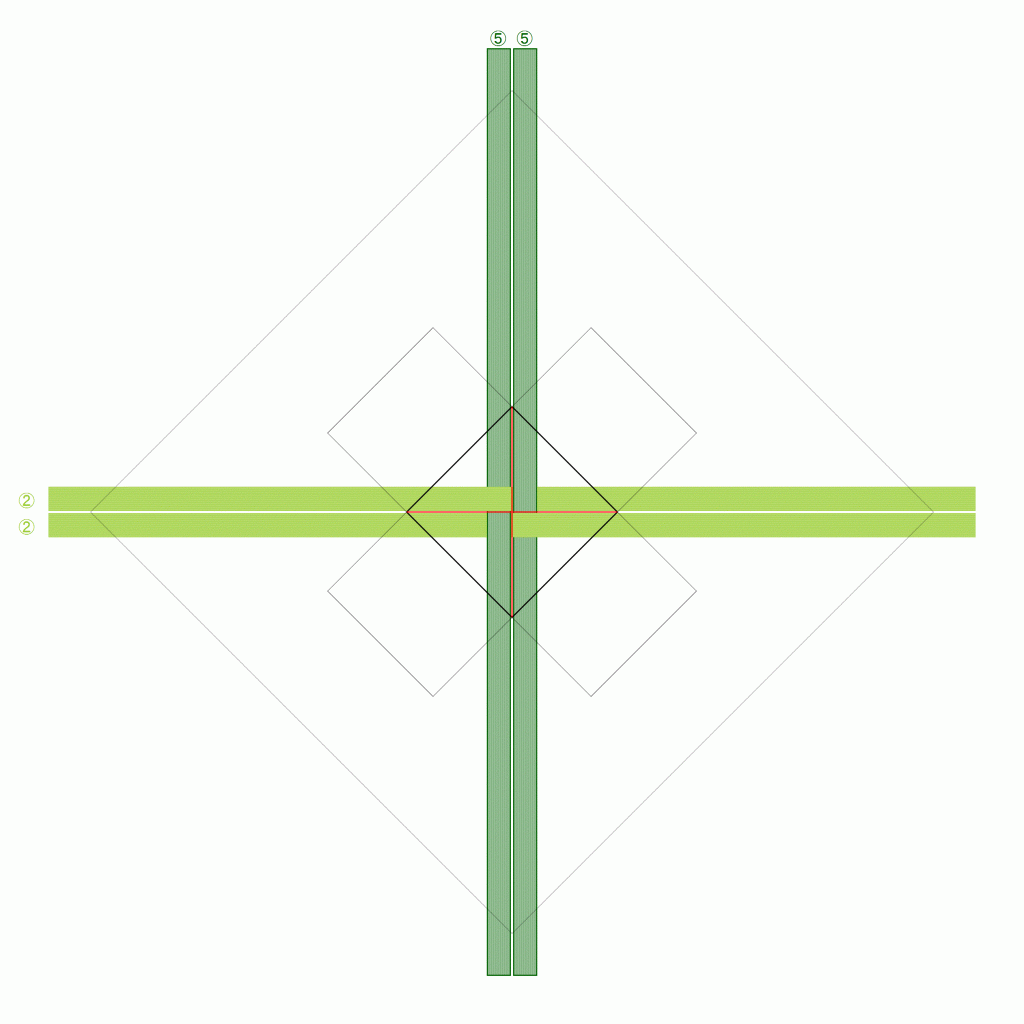
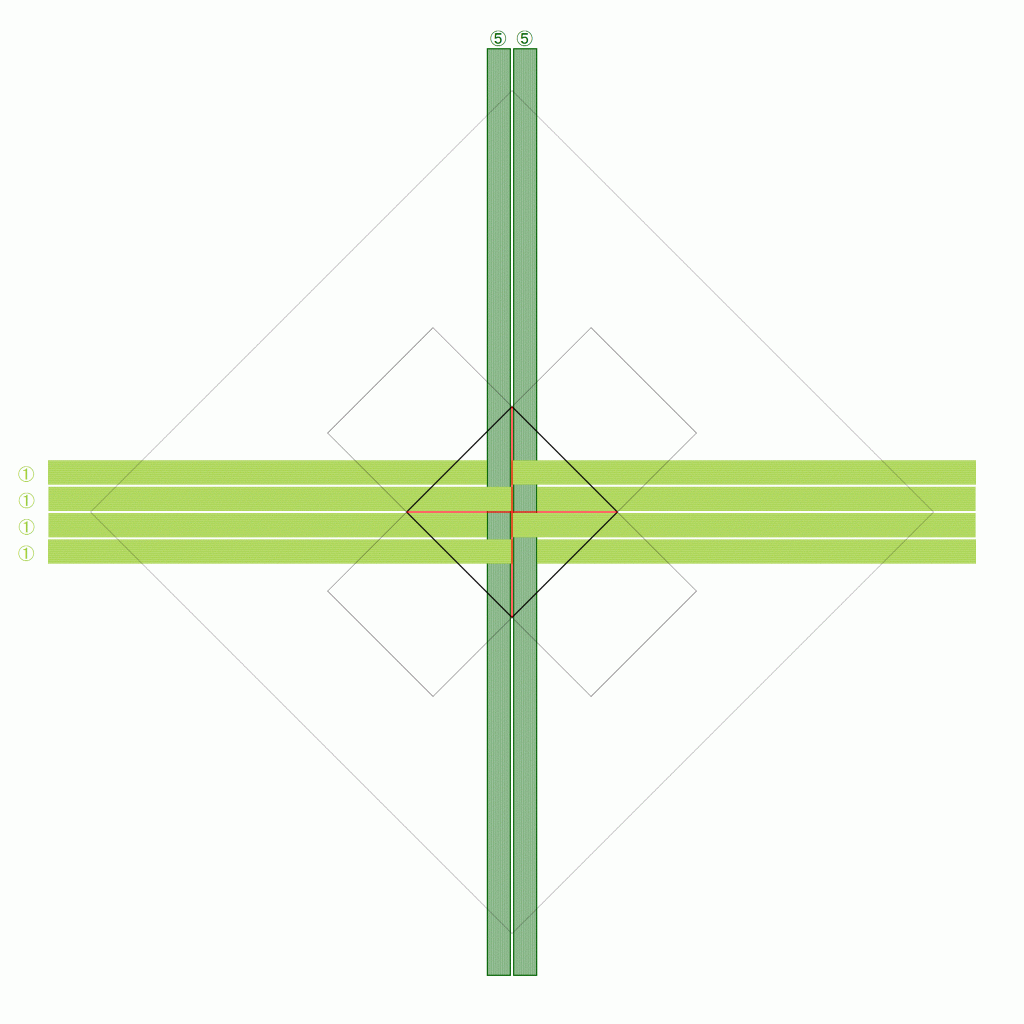
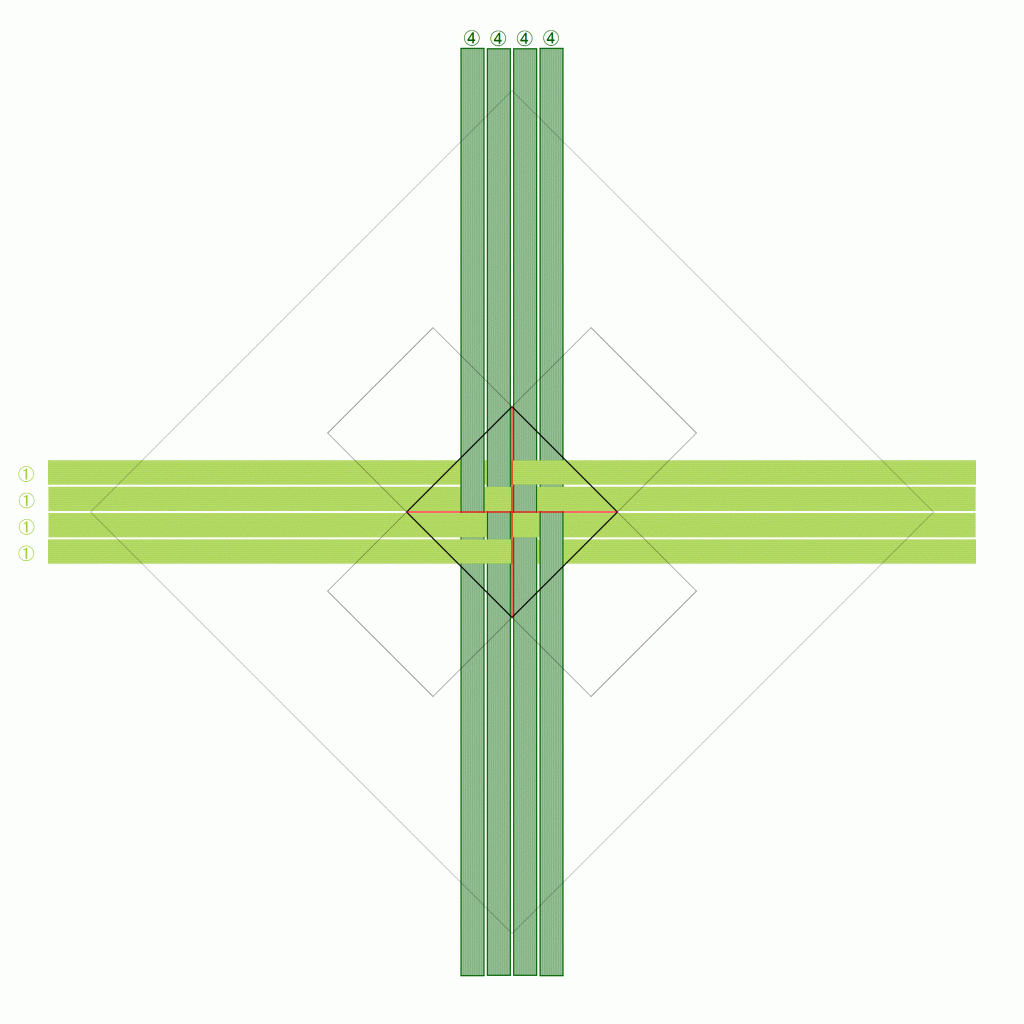
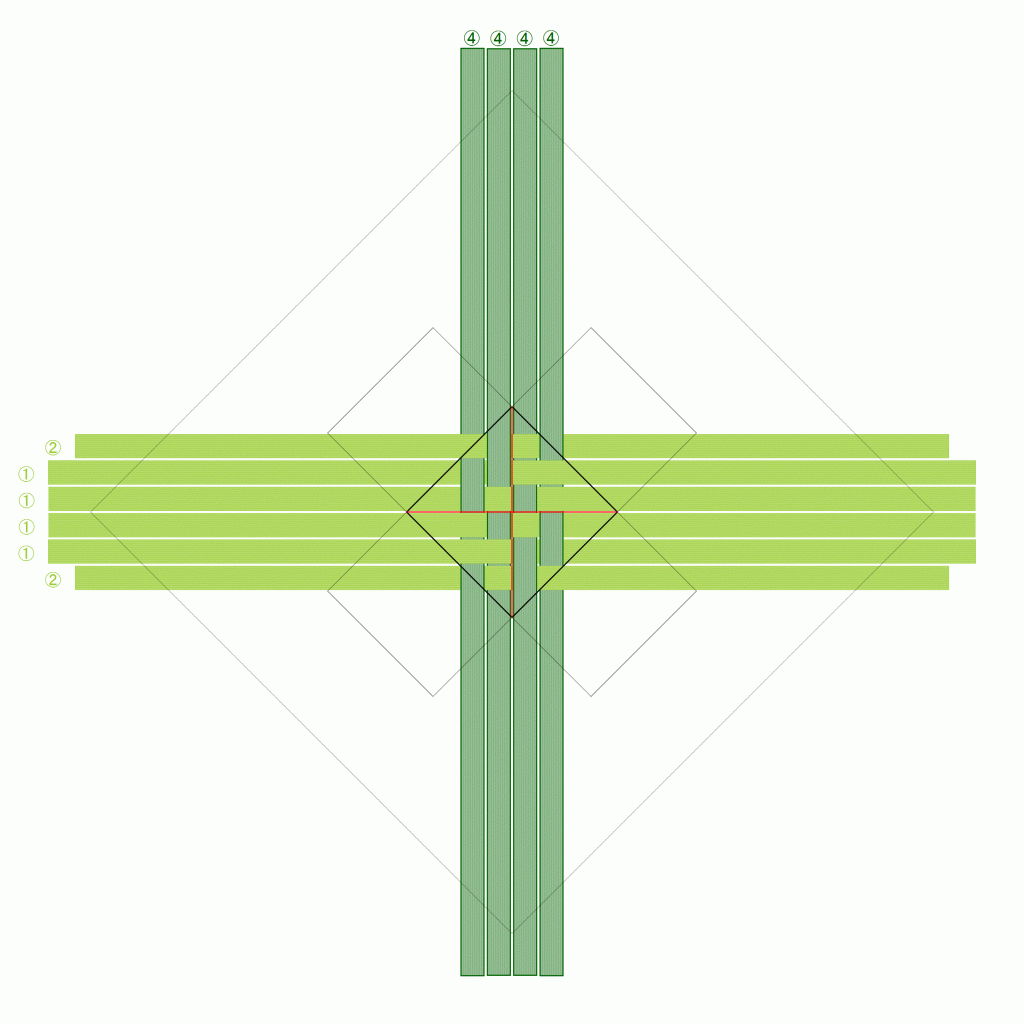
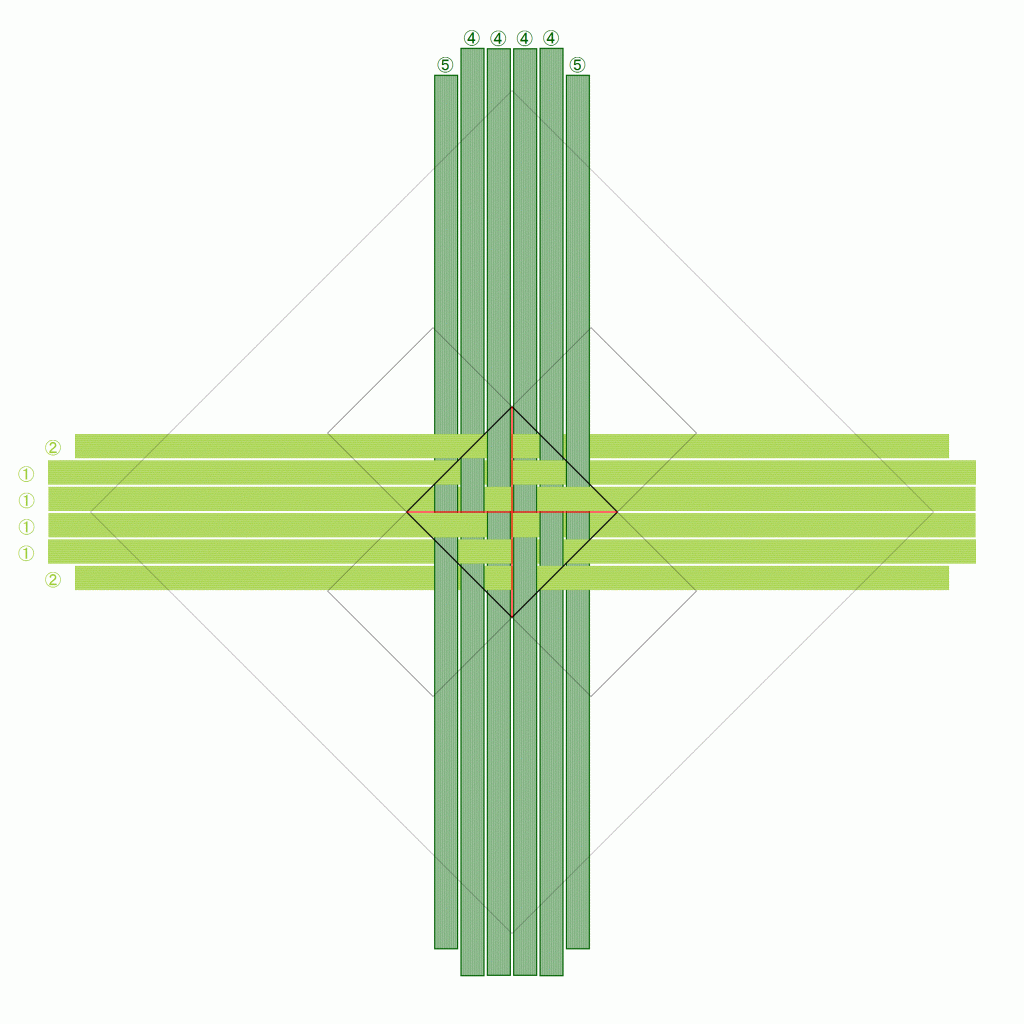
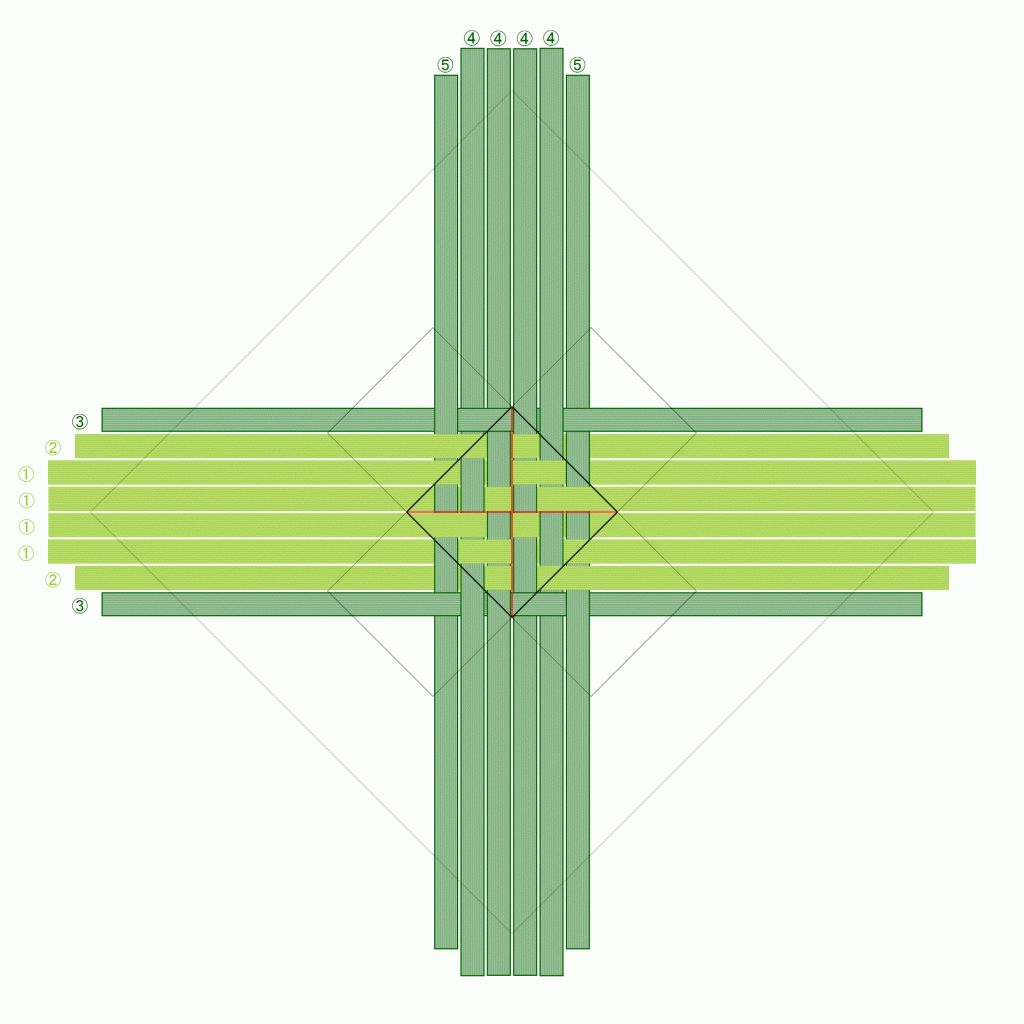
正確には、「折りカラー編み」としてではなく、その最もシンプルな適用例である「籠」としての出願ですが、今までにない編み方であることが正式に証明されたと言ってよいと思います。
出願にあたり、ご教授・相談・アドバイス・チェック・手続きまでご支援くださった INPIT京都府知財総合支援窓口の皆さまに、心よりお礼申し上げます。そして、書類作成を助けてくれたAIにも。
そして、特許を取ったのは、かご編みに携わる皆さまに使っていただくためです。
制限したいからではありません。
折りカラー編みについては、最初のアイデアが3月、出願が5月末です。その間、正方形、長方形、そして高さを変えてと適用範囲を広げつつ、またその試作や検証・命名のプロセスはすべてブログで公開してきました。特許出願を決めたのは、考え方、計算式、適用方法がまとまり、手順書やYouTube動画として公開した後のことです。
本来、「世に知られていないこと」が特許の前提ですから、ここまで公開してきたものは難しいと言われました。それでも「新規性喪失の例外」を適用すれば可能性はあるということで、公開の証明書を山ほど添付しながら出願しました。
では、なぜそこまでして出願したのか。
理由は、誰も、新しい編み方だと思ってくれなかったからです。
何十人もの方に、試作品をお見せし、使ってくださるという方には差し上げてきましたが、編み方について尋ねられたことは一度もありません。疑問は皆無。私にとっては「今までにない」のに、皆さんには「よくある普通のかご」「あたりまえの格子模様」でしかないらしいのです。
あまりの“普通” 扱いに、改めて、完成したかごを見ると、内側も外側も同じ編み目が続き、不自然な継ぎ目も、難所もありません。模様の変化を見ながら作った私と、完成品だけを手にする方との間に、認識の差があるのだと気付きました。
折りカラー編みは完成した技法ではなく、まだ可能性の“種”の段階にあると思っています。実際、出願後も、別の配置パターンが見つかったり、他の模様に応用できることがわかりました。編む方が増えれば、もっといろいろなアイデアが出てくるでしょう。
でも、よくある普通のかごなんて、誰もわざわざ作ろうなんて思いません。だからこそ、特許という形で「これは新しい編み方なのですよ」と示すことが、
“それなら一度試してみようか”
と思ってもらうきっかけになると考えました。
今回の特許は、技法を縛るためではなく、“新しい” と気づいていただき、試してみようと思っていただくためのものです。かご編みにおけるひとつの“種”として、自由な発想で試し、育てていただければ嬉しいです。
そしていつか、この編み方が手法の一つとして自然に使われる、特別ではない、「普通の編み方」となる未来を、静かに夢見ています。
先とはちょっと違うタイプの和紙で試してみました。薄くて、透かすと繊維の筋が見えるやわらかい和紙です。
同じように芯を入れようとしてみたのですが、透けるし何重にも巻くとかえって形が整いにくい。結局、芯は入れずに、10センチほどに細切りにした和紙を、1.5センチ幅の紙バンドを型紙にして、テープ状に折って使いました。
1本のテープがおおよそ6重ですから全体が24重以上になるわけですが、厚さを測ると1.6ミリ・押し付けて1.2ミリ、先の箱の半分でした。編み地も柔らかくて、厚手のフェルトのような感じといいましょうか、形を変えても折り目がつきにくく伸ばせば戻ります。
箱にはちょっと頼りない感じですし持ち味の透け感もありませんが、それなりの強度はあり畳むこともできる、そんな用途があれば、使えるかもしれません。
データです。
先と同じ、80cm×55cmの和紙を2枚使って縞模様の小物入れにしてみました。友禅紙とうるし紙です。
縦横の四角数がともに４ですから、どんな高さでも縞模様になります。でも、整数で色を変えるより、小数0.5で同色に重ねた方が綺麗に折り返せるので、高さを2.5にしました。
実は、先と同じ幅で80cmだと、作れるのは高さ2までなのです。でも、同色に重ねるのであれば多少短くても模様に影響ありませんので、芯地幅を少し細めの24mmで作りました。
芯地に合わせればテープにするのもそう手間はかかりませんし、和紙のカットもざっくりで済みます。すべて外側への折り返しなのでわりと簡単でした。
データです。
芯地は先に添付のcoreを使ってください。
包装紙で箱を作れるなら、和紙ではどうでしょう。
80cm×55cmの和紙を2枚使って、格子/市松模様の小物入れにしてみました。折って編んで差し込んだだけで、糊は使っていません。
A4の画用紙を2枚、各、26mm幅8本にカットして和紙でくるみ、テープ状にしたものを編みました。幅合わせ兼補強です。耐久性に期待して、縁や底辺はうるし紙になるようにしました。
縦横の四角数を、３にして単位を大きくするか、４にして作りやすくするかを迷ったのですが、半分の繰り返しで作れる４を選びました。
底と内側です。側面の角は折らずに丸みをつけていますが、折って四角い箱にするのもありでしょう。
データです。
芯地の幅は26mmにしましたが、25mm・26mm・24mmの３サイズが作れる用紙を添付しておきます。同サイズを2枚印刷すると、8本×2が切り取れます。
