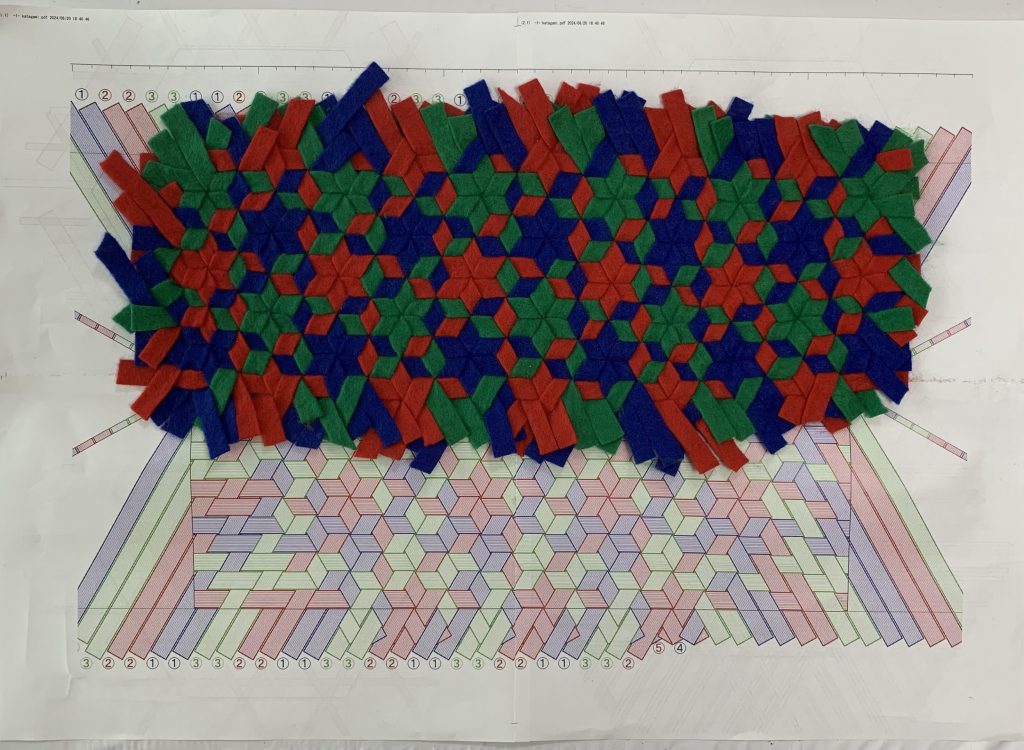
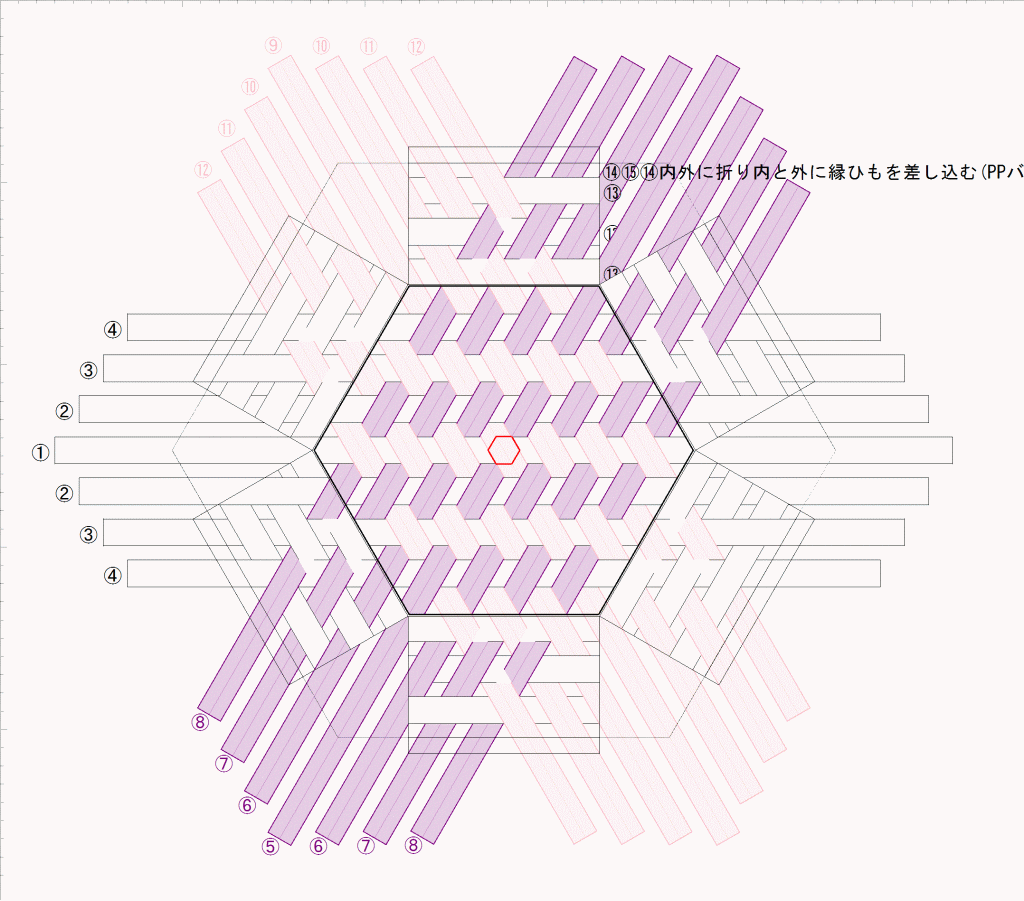
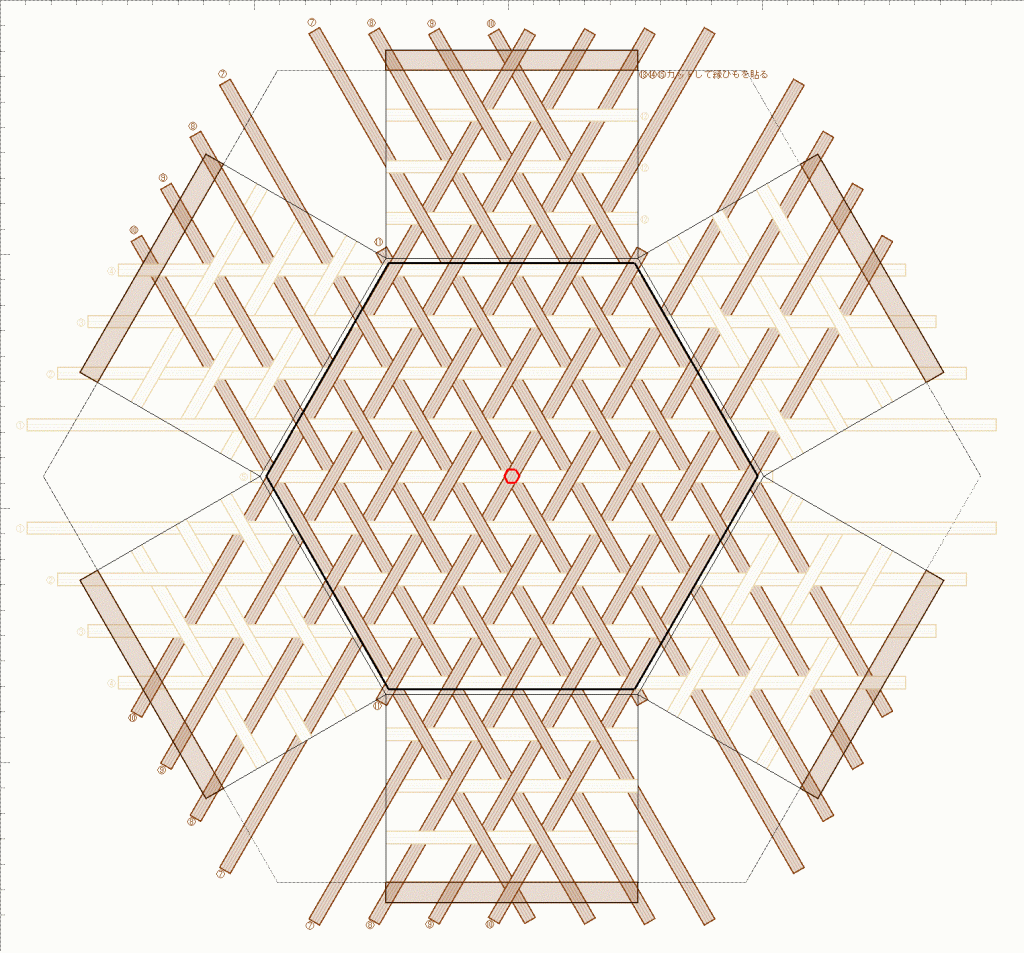
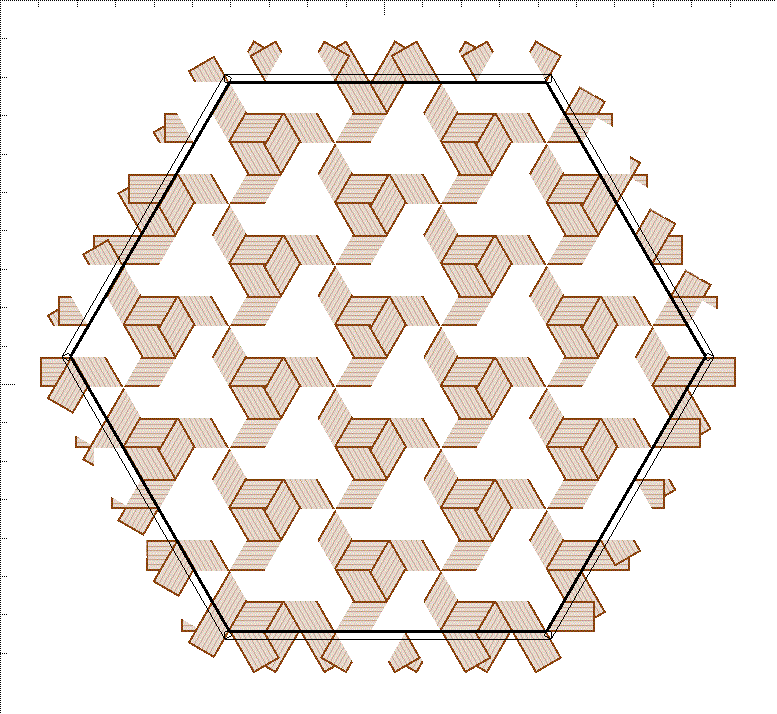
2色パターンでもうひとつ、作ってみました。単純な繰り返しです。
位置 | 横ひも | 斜め60度 | 斜め120度 |
|---|
| -1 | A色 | A色 | A色 |
| +1 | B色 | B色 | B色 |
各辺、左右対称にはならず、色も底から続きません。側面の模様は崩れてしまうので、浅いかごにしました。
 鉄線編みの浅かご、1本ごと2色
鉄線編みの浅かご、1本ごと2色
底です。
 鉄線編みの浅かご、1本ごと2色の底
鉄線編みの浅かご、1本ごと2色の底
すき間が不均一ですが、でも、今回は、ちゃんと正六角形になりました。まず六つ目を作る、という方法で作ったからです。
こちらの文献、
「HEX WEAVE & MAD WEAVE」An Introduction to Triaxial Weaving,
Elizabeth Lang-Harris & Charlene St. John, 2014, Schiffer Publishing ,
ISBN: 978-0-7643-4465-7
46~49ページに、図とともに、作り方のSTEPが載っています。
- STEP1 六つ目を1枚作る
- STEP2 もう一枚の六つ目を作る
- STEP3 2枚の六つ目を、入れ子に重ねる
- STEP4 真ん中の空いた位置に横ひもを差す
- STEP5 更に横ひもを差す
- STEP6 120度の真ん中空き位置に斜めひもを差す
- STEP7 更に120度の斜めひもを差す
- STEP8 60度の真ん中空き位置に斜めひもを差す
- STEP9 更に60度の斜めひもを差す
大きな分かりやすいカラーの図です。
なるほど、どのみち最初に六つ目を作るんだったら、2枚作った方がもっと簡単だよね。型紙だからずれないし。
でも、説明文は読まずに図だけを見て試したものだから、何度も作っては外し…..やり直しの連続でした。
- 単に3本ごと3方向に分けただけではダメ。三角になって、六つ目になりません
- 適当な六つ目3枚に分けただけではダメ。どう重ねても重なりません
- 六つ目枠と、その中の下向き三角に分けてもダメ。作りたい模様になりません
ポイントは、亀甲パターンの位置にある六つ目に分けること、だったのです。
掲載されている図は、3枚が分かりやすいように色を変えたのだと思ってました。だから「3つに分ければいいのね」と読み取ってしまったのですが、色そのものに意味があったのでした。その先のページには「spot form」として亀甲模様の写真が3枚も載っているし、ちゃんと説明されていたのかも。。。紙の本は、自動翻訳されないんです。
最終的に、どんな作り方をしたのかは次稿で。とりあえず、このかごのデータです。
追記
このやり方で、既に鉄線編みを作られている方がいました。サイト「クラフトバンド部」のuniさんです。研究ノートとして様々な模様を作られており、YouTubeの動画も作られています。上の文章よりずっとわかりやすいです。リンクはその最初のものですが、サイトやYouTubeチャンネルには他にもたくさん掲載されています。