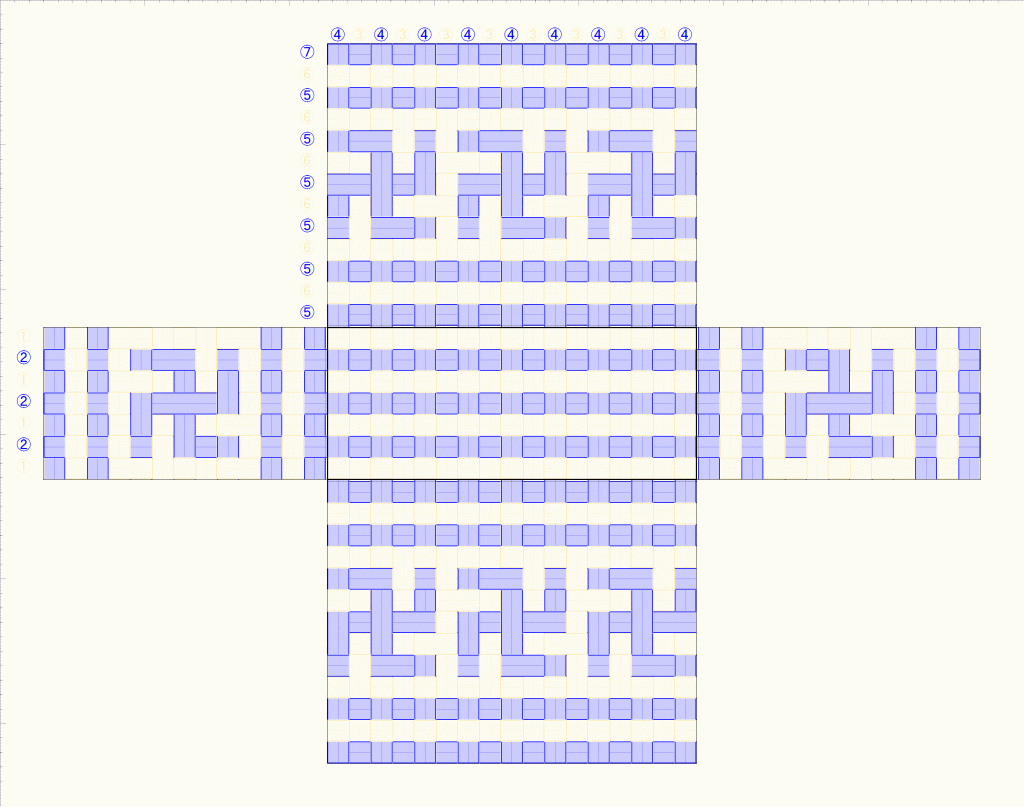
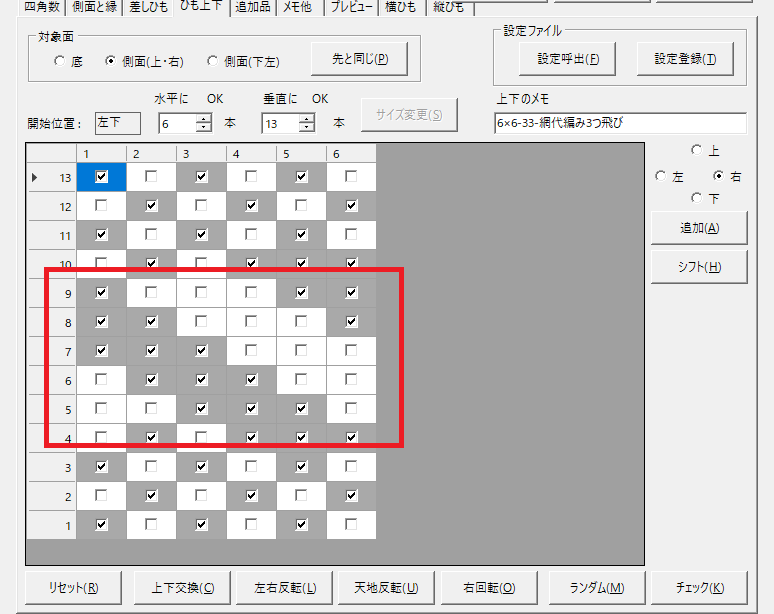
網代編みのかごで、上下を2×2にしておけば、真ん中部分はかなり自由に作れそう、ということがわかりました。そこで、同じ段数で、3つ飛びの網代編みで模様を作ってみました。3の倍数にするため縦ひもは2本増やしています。
最終的に作ったかごは、こんなです。
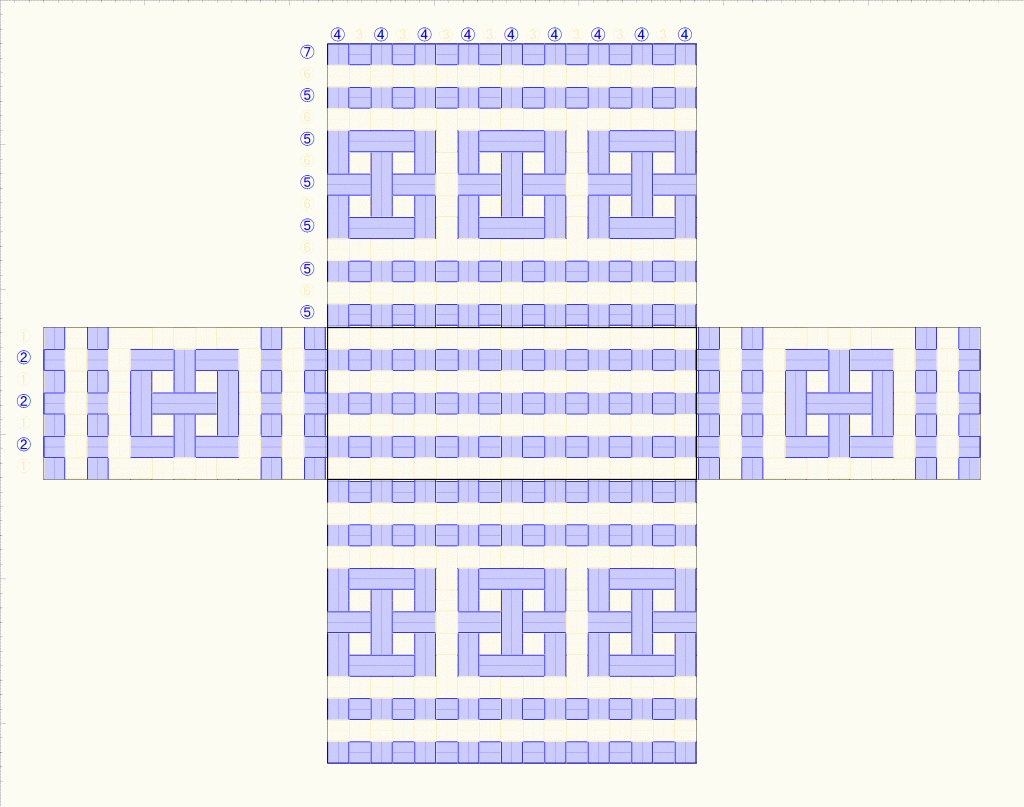
 網代編み模様
網代編み模様
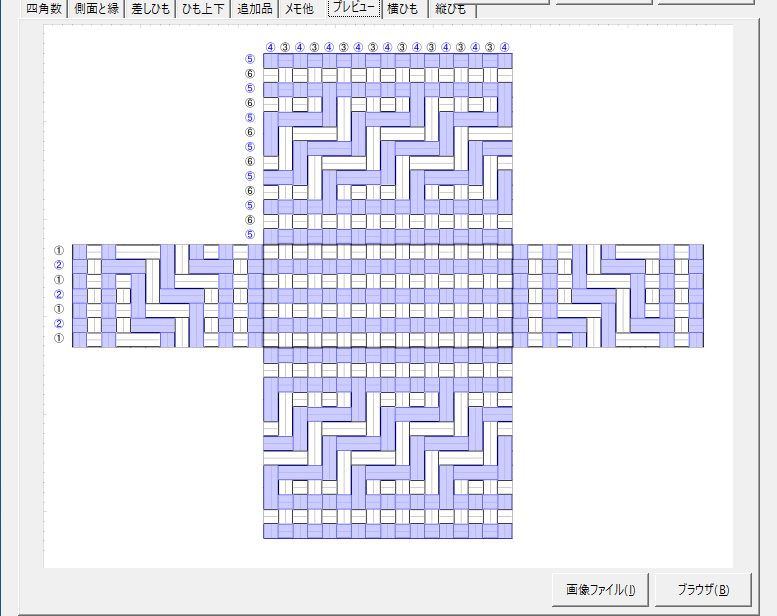
CraftBandSquareの「ひも上下」で赤枠で囲ったところが3つ飛びの網代編みになっています。そのパターンによるプレビュー図が右側です。
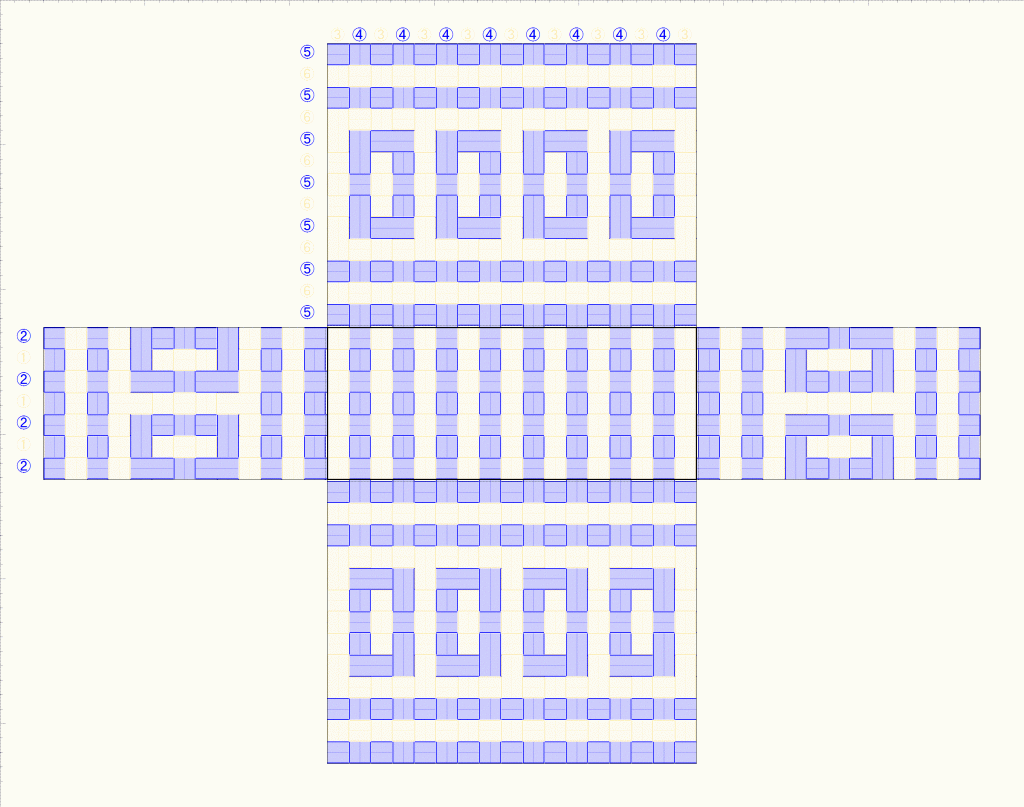
でも、プレビュー図を見ていて、同じ模様を、3本飛びより減らせると思ったのです。2色で作っていますから、縦横同じ色が重なっている箇所は、どちらを上にしても模様は同じです。3つ飛びより2つ飛び、更には1つの方が、かごとしてはしっかりします。
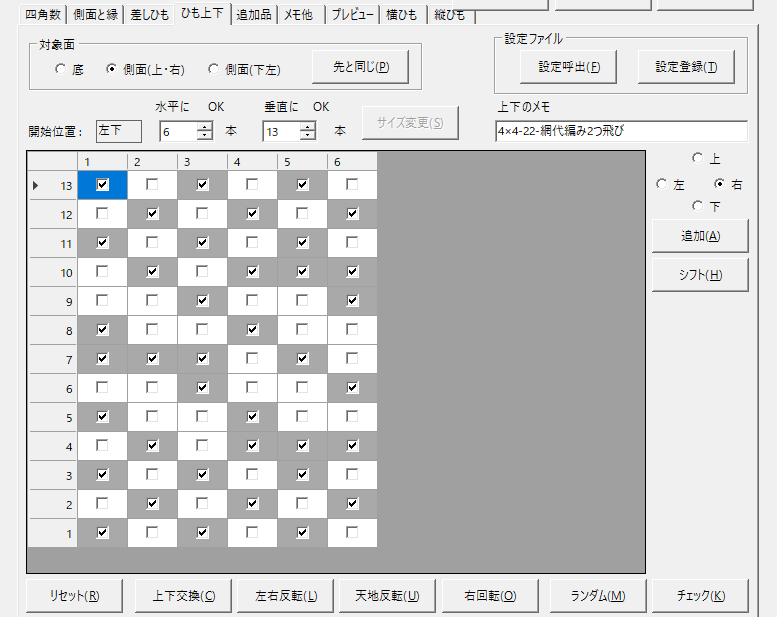
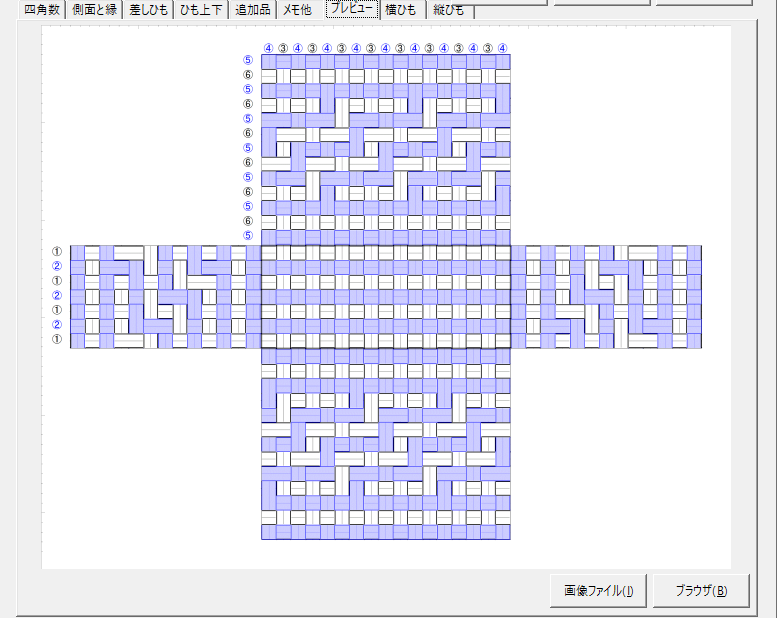
そこで、プレビュー図とひも上下パターンを見比べながら、飛び数を減らすように上下を入れ替えてみました。それがこちら。
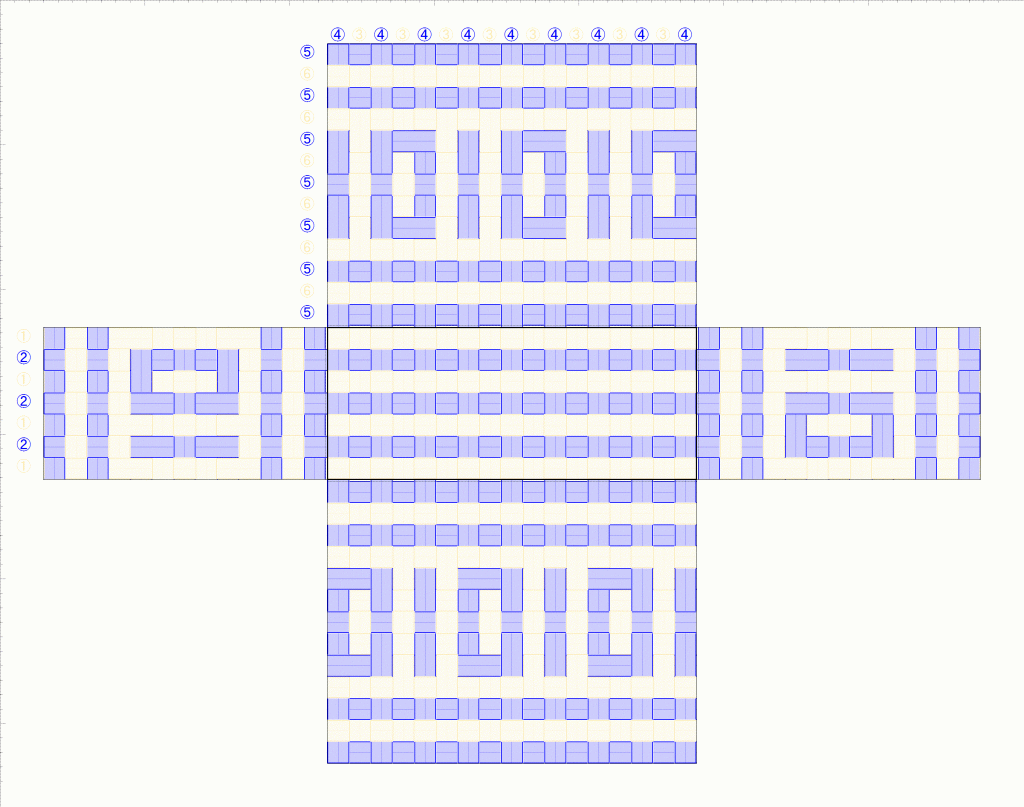
3つ飛びを使わずに、すべての模様を2つ飛びに置き換えられるのか?というのは4色問題みたいなものでしょうか。だいぶ減らすことはできましたが、もっと減らせるパターンがあるのかもしれません。編み目は変わっていますが、2色で見た時の模様は同じです。
そうやって作ったのが、上の写真のかごというわけです。模様は3つ飛び、編み目は2つ飛びの網代模様。
データをつけておきます。ただしこのデータ、縁の代わりに編みひもを表示させた、上図用のデータです。このデータをもとにかごを作る際は、側面の編みひもを縁の始末に置き換えてください。