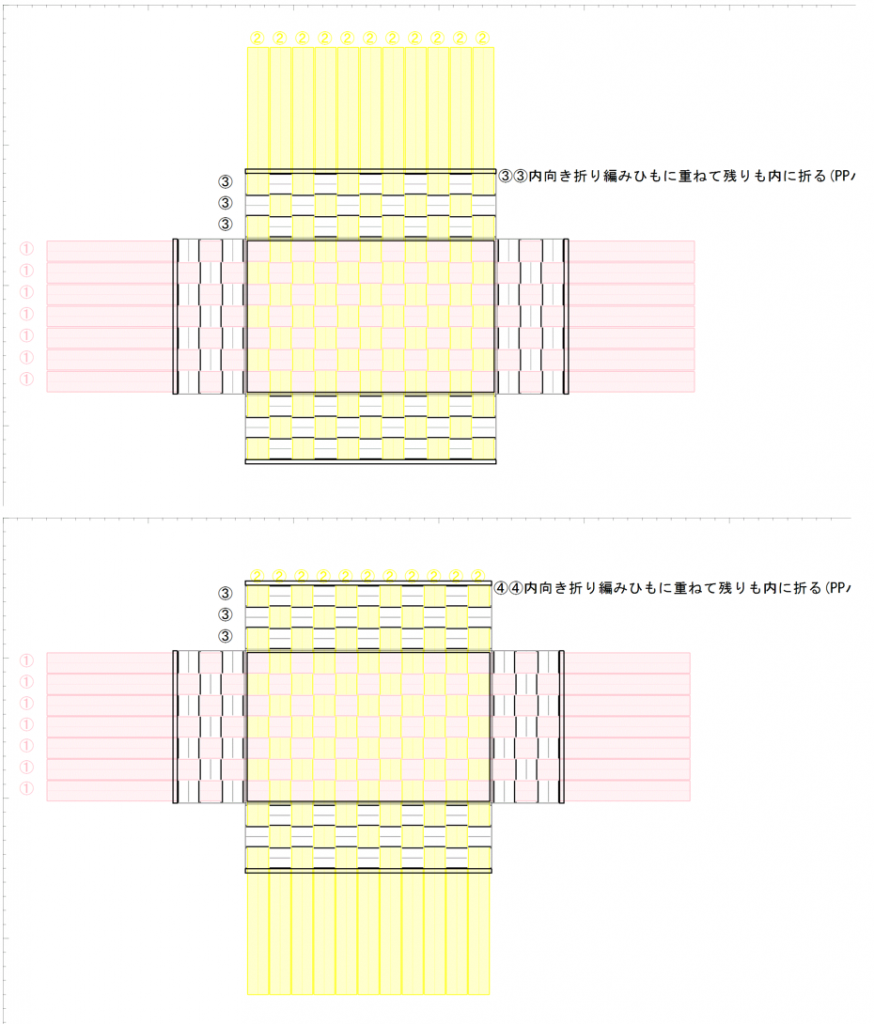
先に、『折りカラー編み(OriColorWeave)』斜め編みの高さとして、「縦横の両端、ひとつ変えるごとに高さがひとつずつ低くなる」という経験則をあげました。
いくつ変えるのか、という点数を整数 N とすると、
0 ≦ N ≦ (縦の四角数 と 横の四角数の小さい方)
であることがわかりました。
Nがゼロというのは、色を変えない、つまり縦ひもと横ひもをそれぞれ別の色にするということです。
Nが1というのは、1点を色替え、つまり両端で計2本の色を替えると、高さが1低くなるということです。
Nが2というのは、2点を色替え、つまり両端で計4本の色を替えると、高さが2低くなるということです。
下図を見ていただくと、その理由がわかるでしょうか。
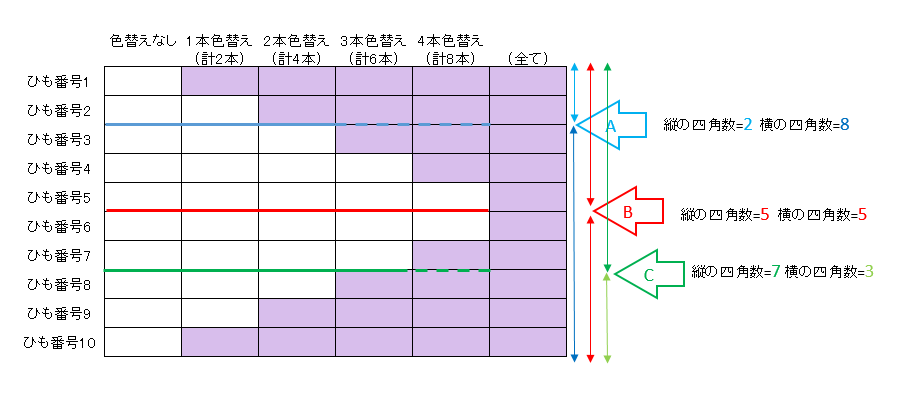
縦ひも数・横ひも数は、ともに縦の四角数+横の四角数です。
例えばこの数が10本とすると、底となる縦横の四角数として可能な組み合わせは、
- 縦の四角数=1 横の四角数9
- 縦の四角数=2 横の四角数8 (上図のAのケース)
- 縦の四角数=3 横の四角数7
- 縦の四角数=4 横の四角数6
- 縦の四角数=5 横の四角数5 (上図のBのケース)
- 縦の四角数=6 横の四角数4
- 縦の四角数=7 横の四角数3 (上図のCのケース)
- 縦の四角数=8横の四角数2
- 縦の四角数=9 横の四角数1
このように、9パターンになります。
N点の色替えで、N×2本が替わりますから、Nの絶対的な上限は(縦の四角数+横の四角数)/2 です。そして、側面に現れてくるブロック模様は、底の長方形の2辺のサイクルですから、この辺の長さ以上の色替えはありません。
底の長方形の2辺の長さというのは、縦の四角数と横の四角数ですから、縦の四角数と横の四角数の小さい方が上限になるわけです。
式によると、変更可能幅が最も大きく、ほぼ任意に作れるのは底が正方形の時。縦の四角数と横の四角数の差が大きくなるほど、作れない高さの範囲が広がるということがわかります。
でも、最も差が大きい、つまり、縦の四角数もしくは横の四角数がゼロの時は、同色ブロックが現れませんから、折りカラー編み自体が必要ないというのも、面白いです。底が長方形である、という条件を満たさないので、対象外であるとはいえ。