縦横とも同じ2色を交互に編んだ場合、模様としては線になります。
でも、斜め組み編みの場合は、角のところで縦横の方向が変わるため、すべてのバンドをそのまま交互にすると、縦横の切り替えが発生します。
線としてつながるように作ってみました。四角数6×6、斜め網代編みと同サイズ、使った色は同じくブラウンとこげ茶です。

内側はこんな感じ。

このかごの底組み図を見ると、底の角4点それぞれ、同じこげ茶のバンドが2本になっています。底の角を中心として、縦・横のバンドの方向が90度変わるため、例えば
- 横のバンドがブラウンであれば → 角を挟む縦の2本のバンドはともにこげ茶
でないと、それぞれの側面において、ブラウンと交互になりません。
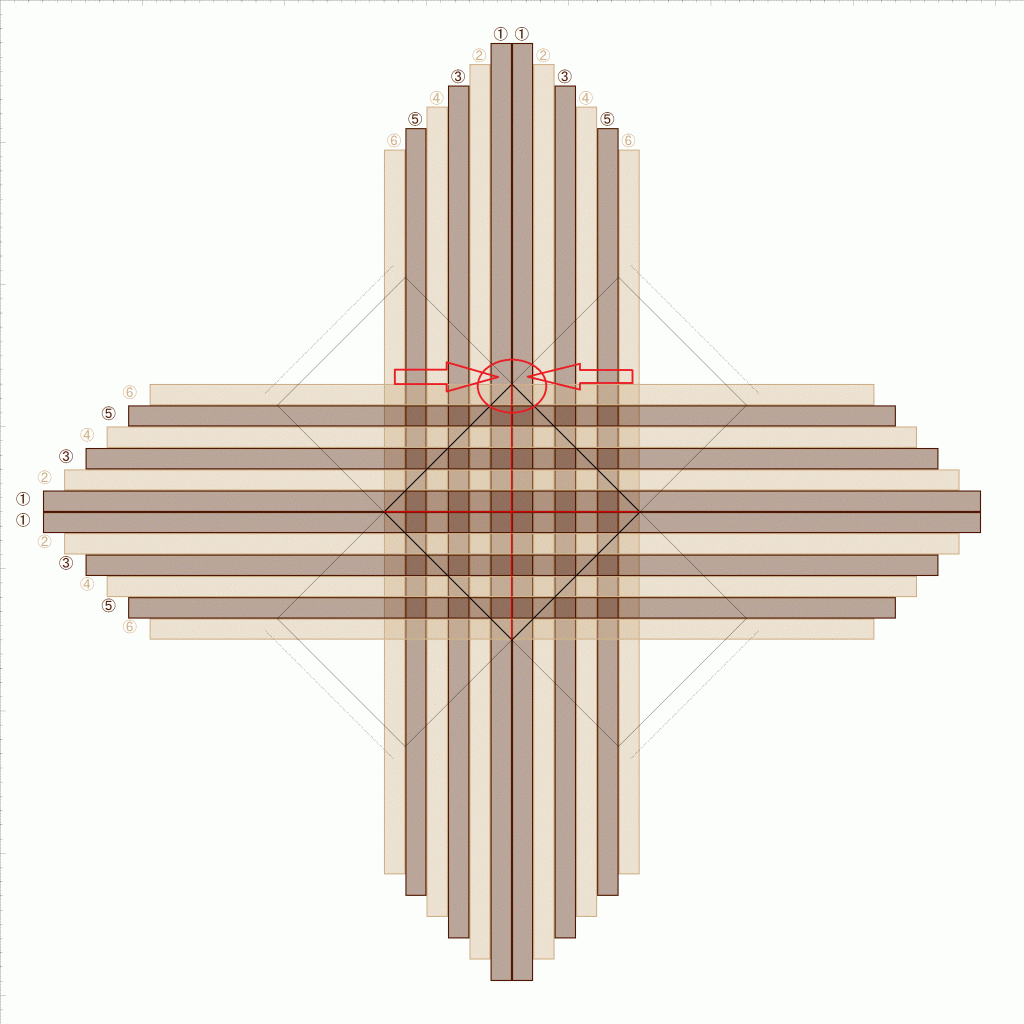
上の赤丸に示す、上の角で縦のこげ茶が2本になるとすると、こげ茶2本が下の角になる必要がありますから、縦の四角数と横の四角数は同数、つまり正方形が条件になります。
また、この例では、縦・横の四角数が6個、つまり偶数ですから、左の角と右の角となる縦バンドの色はブラウン、従って左右の角をはさむ横バンドはこげ茶2本となります。
では、縦・横の四角数が奇数の場合はどうなるか。左右の角となる縦バンドの色はこげ茶になりますので、左右の角をはさむ横バンドはブラウン2本となります。
縦の四角数・横の四角数が奇数(7個)の例です(縦横入れ替わっていますが)。この場合も、立ち上げて組んだ時、線がつながることがわかるかと思います。

結論
線がつながるように作れるのは、縦横同数、つまり正方形の時のみ。
中心に同じ色を重ねるようにバンドを配置しますが、
- 四角数が偶数の場合は、重なる色は、縦・横とも同じ
- 四角数が奇数の場合は、重なる色は、縦・横で異なる
ようにすれば、線がつながる、ということです。
上のかごのデータです。
参考に、7×7(奇数)パターンのデータもつけておきます。