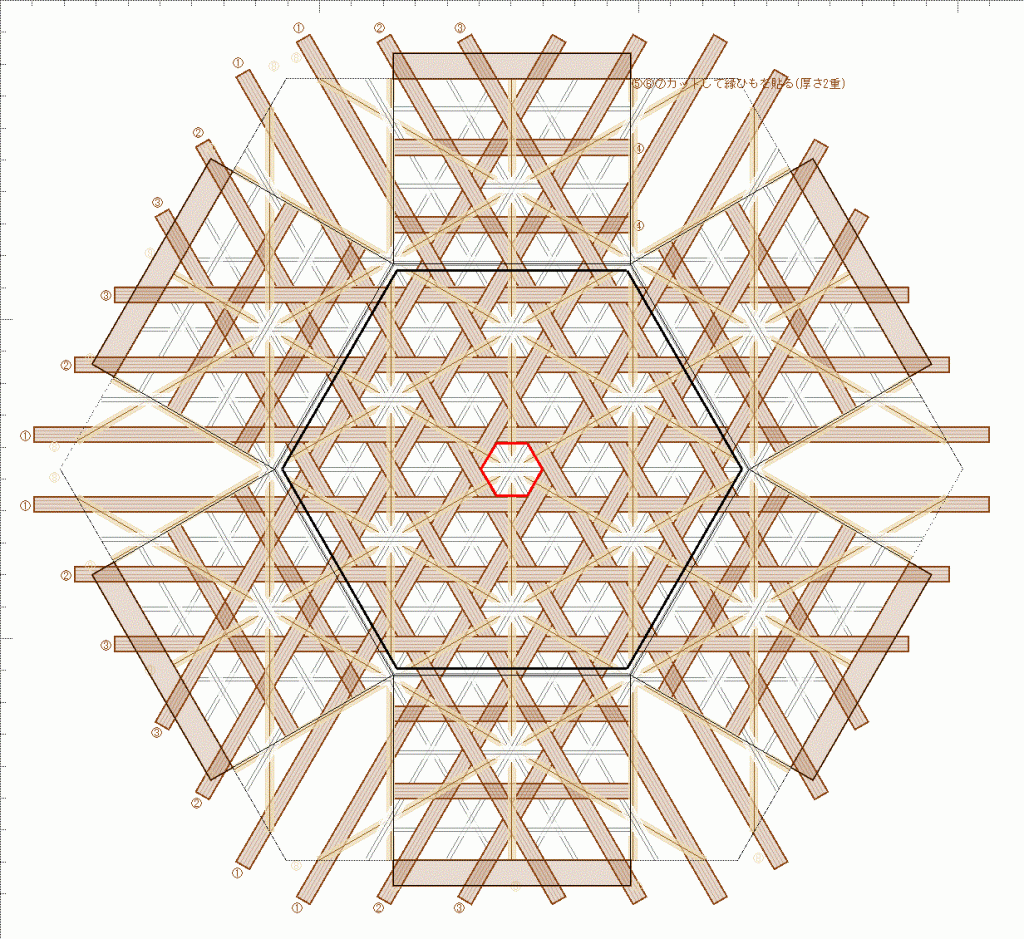
六つ目のかごに、各方向平行な差しひもを加えました。同じ幅のバンドで、目を埋めることができ、すき間のないかごになりました。

縁は2段に重ねました。斜めひも・差しひもとも、折り返しの位置になりますので、そのまま折って重ねています。持ち手もその間に入れました。
底の角 6点はY字分岐になります。底部分のバンドを2枚重ねて、五角形箇所で分岐させました。ちょっと浮いた状態になっています。

図は差しひもが上に重なっていますが、2本のバンドの間を通しました。

データです。
縁の編みかたに「縁ひもを2段置いて差し込む」を追加したので、設定データをつけておきます。