月別アーカイブ: 2023年4月

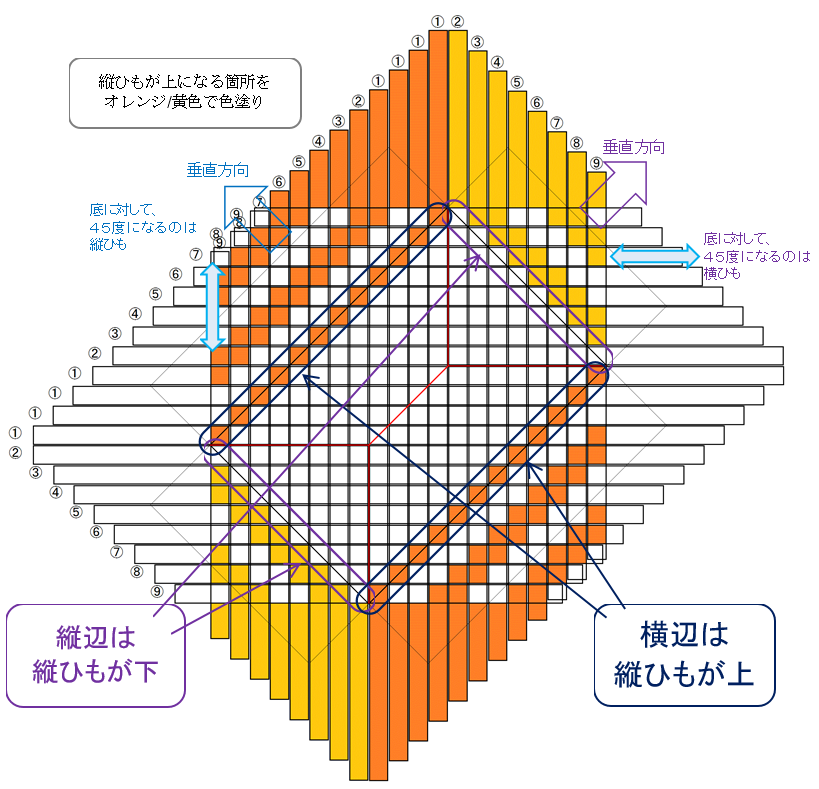
斜め網代編みの底の模様(3)

小さいかご、模様、網代編み

横の線が長く伸びるパターンの底が組めたところで、立ち上げて側面を編み、縁をかがりました。できたかごが、こちらです。

底から見るとこんなです。

どうでしょうか。ちょっとは上達したかな、と言いたいところですが、今回は、先生に教えていただいたのです。アトリエ・プチ・マロウのバスケット部、私にとって初めての教室です。

ゆがみを整形するためにはボンドでの固定は最後にした方がいい、だからこれで底の4隅の角を留めてください、と渡されたのがヘアピン。型紙に書かれていた底の延長線を目安に留めたのですが、位置を1本分、間違っていました。先生から、その位置ではパターンがつながらないとの指摘があり修正できましたが。

また、折り位置に霧を吹き、手でなじませてから立ち上げること、まず角・次に1～2段づつんで組んでいくこと、などを教えていただきました。側面を編む際のひもの固定には、先までしっかり留まるワニ口クリップが良いということで貸していただき、確かに、指先が挟まれても簡単には抜けないくらい、しっかり留まることを体感しました。

すき間が空いていたり歪んでいたりすると、先生が目打ちを使って直してくださるのですが、すごく手が早くて、え？今何をされたの？どこがどうなったの？と思っているうちに、見ると、魔法のようにきれいになっているのです。

ということで、先生の手をお借りしてですが、横の模様を優先した斜め網代編みのかご、形にすることができました。

作ってみてわかったこともあります。横に模様が長く揃ったことで、蛇腹/アコーディオンみたいに伸び縮みするのです。最後に縁をボンドで固めることで、だいぶ固定されますが、途中は力を入れ過ぎないようにしないと形が変わりやすい。底の中央線で4分割というルールには、4方向に分散することで固定に役立つ機能もあるのだなと、改めて理解しました。

データはこちらです。

Square45(6)220-130-60ダウンロード

斜め網代編みの底の模様(2)

小さいかご、網代編み

先に計画した、斜め網代編みで横の線が長く伸びるパターン、作ってみました。

CraftBandSquare45で型紙を作り、模様がわかりやすいよう、縦ひもと横ひもの2色にしました。

色つき小かごでは、端から始めたら最後が足りなくなってきたので、普通に真ん中のひもから始めてみました。最初に中央の縦ひも2本・横ひも2本を組んで、上下左右に順に増やしていきました。

でも、上下左右に増やしていくには、何度もひもをめくって型紙の色をチェックする必要がありました。つくりを理解して差しているわけではないので、少しずれると上下がわからなくなってしまいます。結局、全体をプリントアウトしたA4の図を隣に置いて、その図を見た方がやり易かったのでした。

ひものすき間は、色つき小かごの0.2mmでは小さすぎたので、今回は0.4mmとし、ほぼその通り配置できています。であれば、

最初にすべての横ひもを並べる → 縦ひもを端から順に差していく

ということができたのでしょうか。素人にとってはその方がずっと簡単です。

そしてもうひとつ。今回作ろうとしているのは、長方形・底メイン・側面スルーの浅いかごです。横が長いのです。その場合、縦ひもと横ひもが組み合わさってできる正方形がフルに形作られない、ということがわかりました。

上の図でいうと、

  • 右上・左下については、縦ひもと横ひもが完全にクロスしており、三角形が形作られている
  • 左上・右下については、三角形に至らず切れており、台形の状態。

底組みの段階で、縦ひもと横ひもがクロスして組まれた部分は、側面を折って立ち上げた後もそのまま使われます。きれいに側面を組むためには、この三角形の箇所を崩さず保持することが重要だと思うのです。

でもその三角形がフルではなく部分的にしか作られていないので、底の段階でも縦ひもと横ひもが外れやすいし、立ち上げて側面を編むときは、崩れないよう注意する必要がありそうです。

斜め網代編みの底の模様(1)

小さいかご、網代編み

斜め網代編みの底の組み方では、側面のひもの方向を合わせるために、底の中央線で4分割された領域を、それぞれが接する側面に合わせる、というルールにしました。

意図としては、側面の整合性を優先し、底はとりあえずつながれば良しって感じです。バッグの底のように、普通は隠れていて、ことさら見るようなものでなければ、底の模様なんてどうでもよいのです。

でも、浅くて底がひろいかごだったり、入れ子の箱のふたにするなら、どうでもよくなくなってきます。模様が重要になってくるのです。

では、側面のひもの方向を合わせるために必要なのは、どこまでか。最低限なら、折って底の辺となる四角まででしょう。横辺が縦ひもなら縦辺は横ひも、横辺が横ひもなら縦辺は縦ひもが上になればよい。先の絵に追記してみました。

網代編みの底

そして、その中については、上下は、自由に組み合わせられるのではないでしょうか。
ただし、要注意点としては、

  • 上下1点づつになってしまうと編みにくなる
  • 上上上上…とか、下下下下… と長く続くと構造が弱くなる

といったところでしょうか。

試しに作ってみたのが、次のパターン。

底が横に長く伸びるパターン

横長の箱で、横の線が長く伸びるパターンにしてみました。

原理的に、2つ飛びの線だけで埋めることはできませんので、2つ飛びと3つ飛びの組み合わせになりました。横の線を可能な限り長くし、縦辺との辻褄合わせは辺の四角で行っています。上の要注意点に抵触する箇所も出てきますが、数点なので良しとしましょう。

サイズについては、6本幅を基本とし、縦ひも・横ひもそれぞれがちょうど6メートルに収まるようにしました。

さて、これで、目論見通り作れるものでしょうか。やってみました。

『このサイズ』No.9
ピクニックバスケット「ゆかご」

このサイズ、大きいかご

『このサイズが欲しい!』キャンペーンの当選者No.9 yukaさんのご希望は、ちょっとした小物を収納して飾れるようなかご、です。オーダーされたサイズは

幅20cm、奥行き15cm、高さ15cm(外側)

No.7のドライヤーのかごのうち、小さい方のかご(内かご)を見てイメージされたとのこと。棚の上段に置いて、ラタンのバスケットのような、

  • ワンハンドル
  • 蓋つき(上に乗せるタイプ)
  • コロンとした丸い感じ
  • 中が見えない(すき間が開かない)
  • 蓋は縁取りの部分のデザインで

感じを希望されました。

クラフトバンドは平たい紙でできており、素材としての厚みは難しいため、クラフトバンド風にはなってしまいますけれど、ということでお作りしました。

本体下部のよろい編み、ざっくり感を出したくて最初7本幅で編みましたが、丸くするのが難しく、結局、5本幅と2本幅に割いて重ねることになりました。でもそれで、少し立体感が出たかなと思います。

ピクニックバスケット「ゆかご」

ワンハンドルの持ち手は、枝風に2本で作りました。
こちらが、本体のデータです。「よろい編み(2枚重ね)」という編みかたを追加しています。

yuka_coverダウンロード

蓋は、底と同じ作りだと縦横部分が目立って、裏、という感じになってしまいます。周りの同心楕円的な編み目がメインになるように、縦横部分の面積を減らし、差しひもを2回で計16本とし、楕円の周数を増やしました。

その後、データ的には側面になるのですが、立ち上げずにそのままねじり編みを2周し、垂直ひもを追いかけ編み2周分だけ通してから折り、ひもを貼って蓋裏の縁にしました。ねじり編み部分は、本体と同じ飾り編みでかがります。

本体の高さ、当初7本幅で計算していたのが5本幅になり少し低くなってしまったのですが、蓋に厚みがあるので、トータルとして15センチとなりました。

ふたのデータです。本体が出来てから、本体の縁のサイズに合わせて作成しています。

yuka_bodyダウンロード

追記

yukaさんから使っている様子の写真を送っていただきました。
タイトルの「ピクニックバスケット」はyukaさんに命名いただいたもので、愛称「ゆかご」、yukaさんオリジナルデザインのかごです。
yukaさん、ありがとうございました。

ピクニックバスケット「ゆかご」

四つ畳み編みの要尺とコマ寸法の機能検証

アプリ

四つ畳み編みの要尺とコマ寸法については、どんぐりさんのサイト『日々の楽しみ』の記事『エコクラフト　クラフトバンド　石畳編み　畝幅別必要な長さの算出　ゲージ　recycled pulp tape　gauge』のページに、2幅～12幅全てについて詳細な測定報告が掲載されています。測定方法は動画でも説明されており、とてもわかりやすいです。

どんぐりさんに、craftbandknotの要尺とコマ寸法の機能の検証に、上記データを使わせていただけないかお聞きしたところ、快く了承いだきました。検証したいのは、

  • 既定値の妥当性
  • 係数化のしくみが機能するかどうか
  • 全ての幅ではなく、2～3点だけの測定で済ませられないか

です。

操作手順

1.「バンドの種類」に「１２畝で１．５㎝」を追加登録します。これが、どんぐりさんが使用されたバンドとなります。12畝は12本幅、1.5cmは15mmとして登録します。

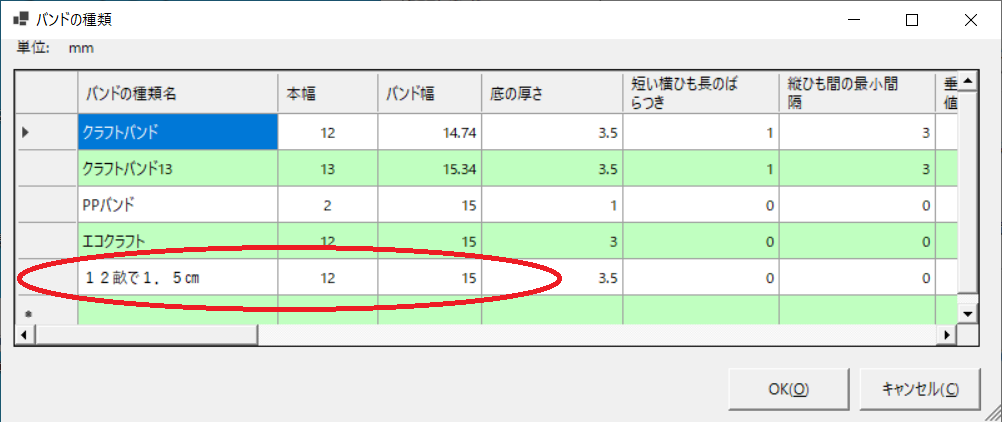バンドの種類に登録

2.「ゲージ」画面を開き、対象バンドの種類名から、1.で登録した「１２畝で１．５㎝」を選択すると、コマ寸法計算値とコマ要尺計算値に、値が表示されています。これが既定値となります。これをどんぐりさんが測定された値(以降、測定値と記載します)と比較してみます。

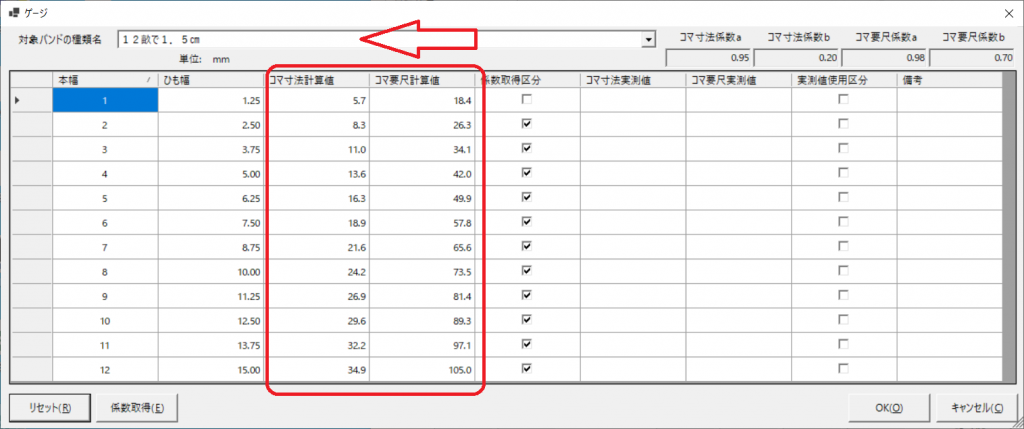既定値

3.測定値を、対応する本幅(畝)のコマ寸法実測値・コマ要尺実測値のセルに入力し、[係数取得]ボタンをクリックします。その後表示されるコマ寸法計算値とコマ要尺計算値が、全測定値を係数化した値となります。これを測定値と比較してみます。

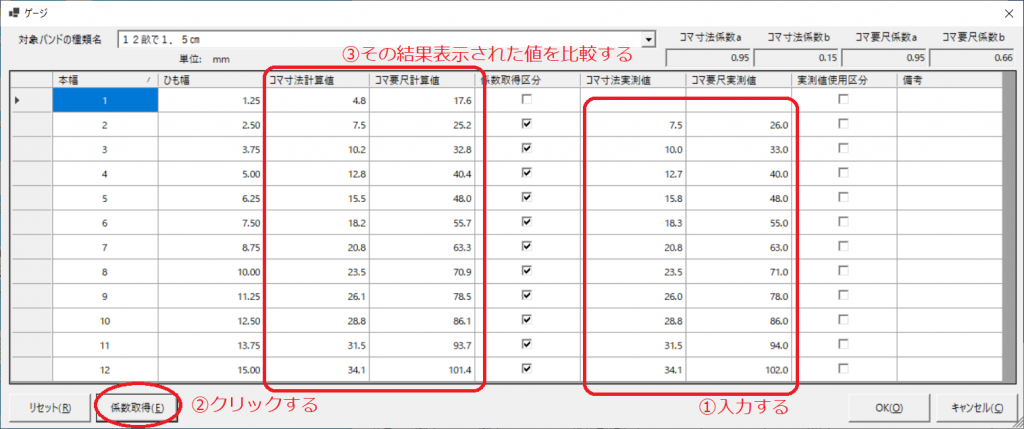全測定値の係数化

3.全ての幅ではなく、2～3点だけの測定をするとしたら、扱いやすいのは、12本幅(そのまま)と6本幅(1/2)と4本幅(1/3)でしょう。この3種類の値を使って係数化してみます。

まず、6幅と12幅のみを係数化してみます。「係数取得区分」の6幅と12幅のチェックをONにし、他はOFFにして、[係数取得]ボタンをクリックします。その後表示されるコマ寸法計算値とコマ要尺計算値が、6幅と12幅の測定値のみを係数化した値となります。これを測定値と比較してみます。

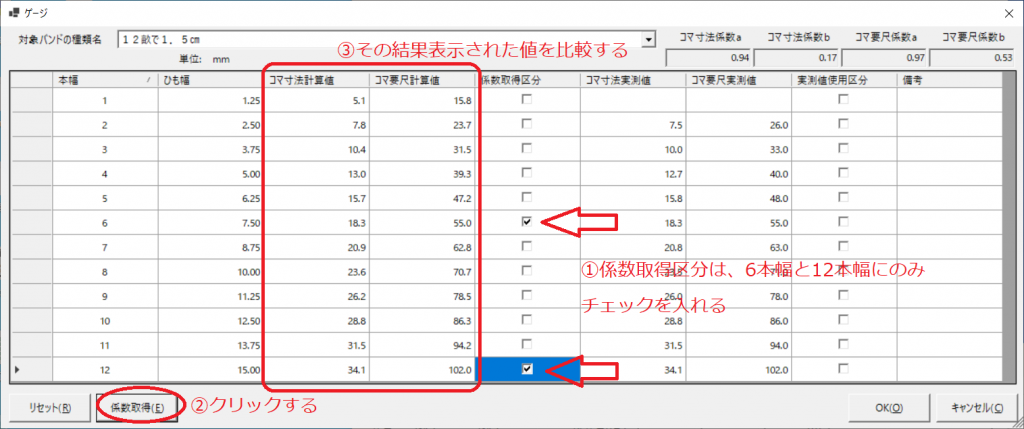6幅と12幅のみを係数化

同様に、

  • 4幅と6幅
  • 4幅と12幅
  • 4幅と6幅と12幅

を係数化し、その結果表示された値を取得します。

実行結果(要尺)

上記の操作により得られた、コマ要尺計算値を測定値と比較してみました。

本幅に対する各値をグラフにするとこうなります。

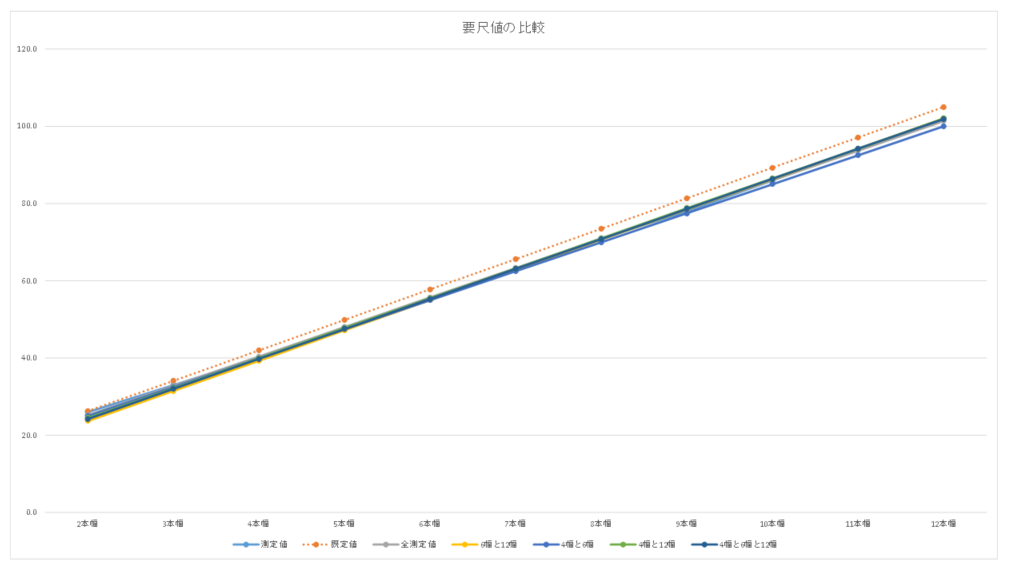
測定値に対して、各計算値がどの程度ずれているかを、(測定値 – 計算値)/測定値　のパーセントで比較してみました。

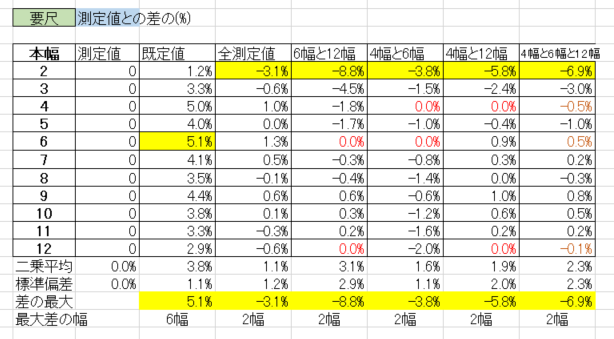
既定値は、最大5%程度の差があります。使用するひもの長さが1メートルであれば5センチ以内ですが、測定値に対してプラス(長め)になっているので、そこそこ使える値、といえるのではないでしょうか。

全測定値を係数化した値は、かなり測定値に近い値になっています。差がいちばん大きいのが2本幅で3%、他はほぼ1%以内に収まっています。

2～3点を係数化した値では、いずれも2幅で差がいちばん大きくなっています。測定値との差が最も小さいのは「4幅と6幅」ですが、12幅の差が2%と多め。全体的に差がちいさいのは「4幅と12幅」で、2幅・3幅以外は1%以下です。「4幅と6幅と12幅」の3点を使っても、精度はあまり上がりません。

実行結果(コマ寸法)

同様に、コマ寸法計算値を測定値と比較してみました。

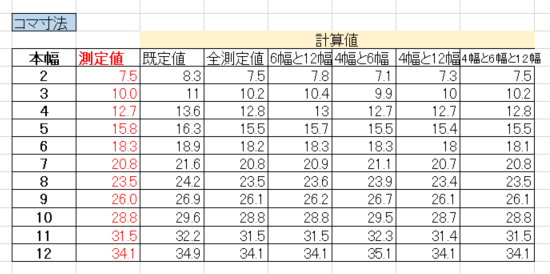
本幅に対する各値をグラフにするとこうなります。

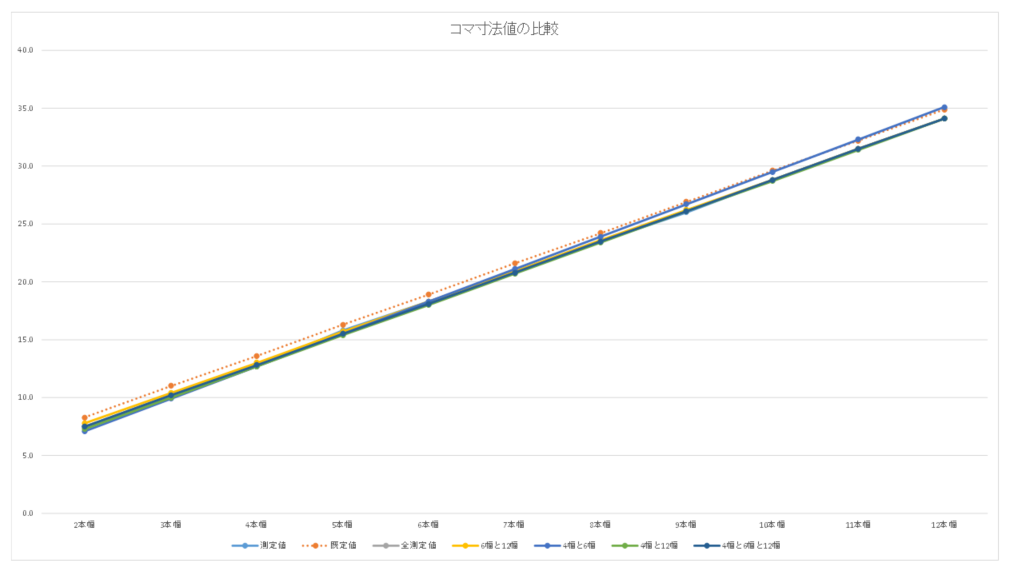
測定値に対して、各計算値がどの程度ずれているかを、(測定値 – 計算値)/測定値　のパーセントで比較した結果です。

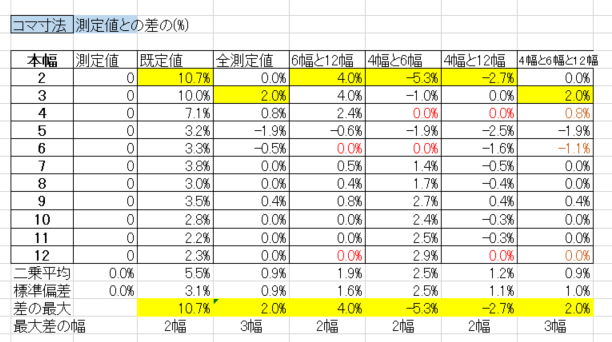
既定値は、最大10%程度の差があります。サイズが20センチとすると2センチ程度ですので、厳密なサイズを得るのは既定値では難しいということです。でも、幅が広くなるにつれ差は小さくなっていきます。

全測定値を係数化した値は、かなり測定値に近い値になっています。差が大きいのは2本幅と5本幅で約2%ですが、他はほぼ1%以内に収まっています。

2～3点を係数化した値では、いずれも2幅で差がいちばん大きくなっています。いちばん測定値との差が小さいのは「4幅と12幅」でほぼ1%以内。「4幅と6幅」は差が2%を越えるものが多い。「4幅と6幅と12幅」の3点を使うと2点より精度はよくなります。

結論

  • バンド幅だけで決まる既定値は、5%程度のずれを見込めるなら、そのままで使用可能。
  • 2幅～12幅の全てを測定すれば、係数化により1%程度の差で値を算出できる。が、測定値が揃っているのにわざわざ係数化する必要はないので、測定値をそのまま保存して計算に使えばいい。
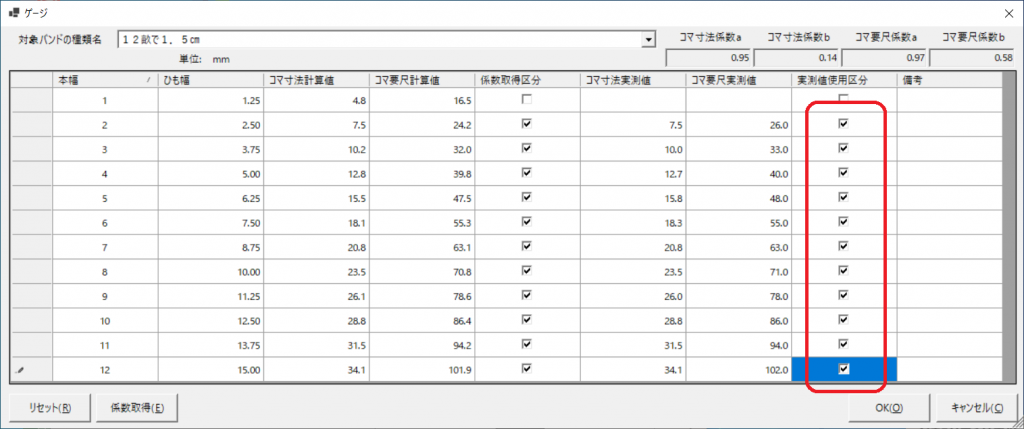測定値を使う設定
  • 簡単に測定するのであれば、以下がおすすめ。
    • 12幅と、4幅と、2幅の要尺とコマ寸法を測る
    • 12幅と4幅の値を係数化し、3幅～12幅についてはその計算結果を使う。差は概ね2%以内。
    • 2幅については、測定値をそのまま使う

こんな設定になります。

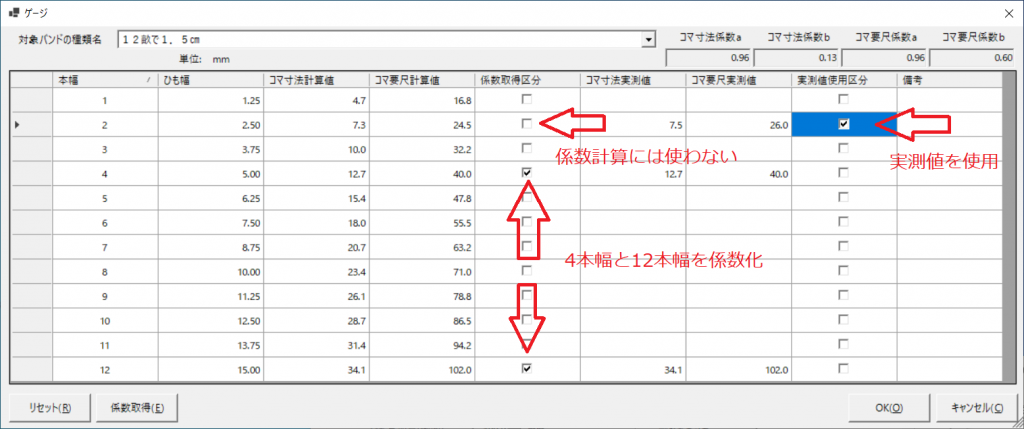
ちなみに、係数化に使った値(4幅と12幅)は、2点の場合、計算値＝実測値となりますので、4幅と12幅の「実測値使用区分」はONでもOFFでもサイズ計算は同じになります。

ということで、検証3点の結果を得ることができました。要尺とコマ寸法を測る手順については、どんぐりさんのページの動画がおすすめです。どんぐりさん、ありがとうございました。

計算結果のエクセルを添付しておきます。

verificationダウンロード