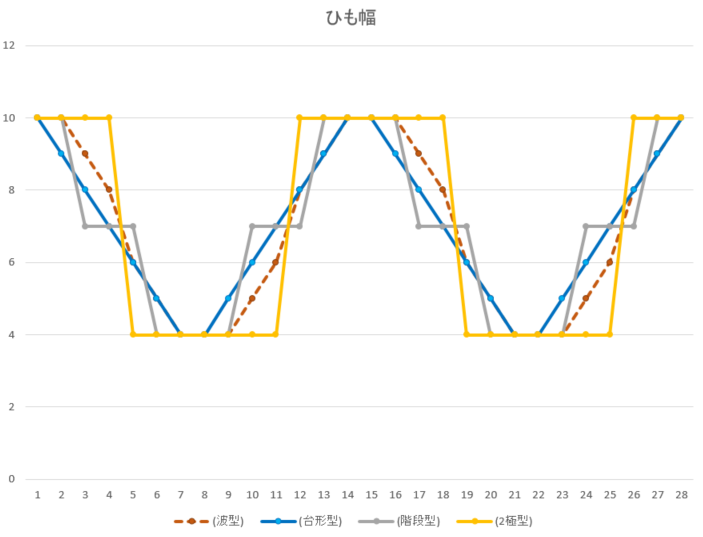
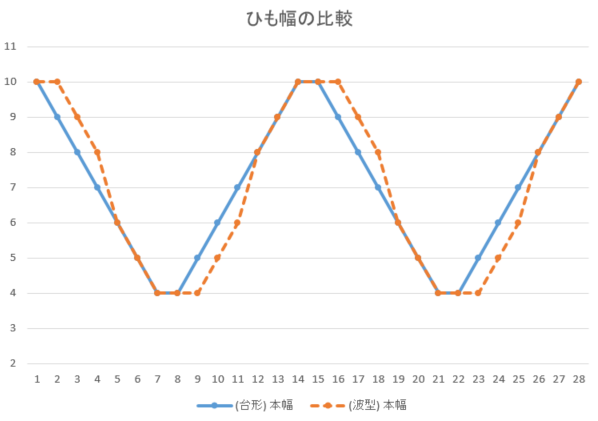
2つ飛び網代編みのボックス、4方向を組み合わせた菱形模様でかごを作ってみました。模様は側面に作り、ひもの色を変えて明確化しました。
底です。2つ飛び網代編み、そのままではやはり無理で、霧を吹いて詰める必要がありました。
PPバンドと逆で、1×1は作りにくく、極力避ける。また、同じ方向にバンドが並列に並ぶと、PPバンドでは重なってしまいますが、厚さのあるクラフトバンド/紙バンドでは不可能ではない。重なりそうになったら、ボンドで貼るという裏技も使えますし。
上側面、重なった個所をマークしてみました。意図したわけではなく、上下の作りが下手だっただけなのですが、こういうパターンもクラフトバンド/紙バンドでは可能とわかったということで、良しとしましょう。
データです。
V1.6ベータ版をテストしてきましたが、V1.6.1 としてリリースしました。
公開はこちら
Release v1.6.1.0のリリース
セットアッププログラムもつけています。既存の3点にプラスして、CraftBandSquare のショートカットが作成されます。
初めてということもあって、波網代編みを試作してみましたが、では、台形(線形)でも、波型(サインカーブ)でも、波模様はあまり変わらないのでしょうか？
考えてみれば、3つ飛び網代編みは、ひもを3本はさみますから、例えば4幅と8幅、2種しかなかったとしても、幅は段階的に変わるのです。こんな風に。
ですので、先の台形型と波型に、更に階段型と2極型を加えて、 CraftBandSquare のデータを作って、模様を比較してみましょう。
比較ついでに、3つ飛びと2つ飛びも比べてみます。こんなデータです。
波型・台形型・階段型・2極型の4つを作って、図を表示させました。
波型、サインカーブに近い形の図です。
台形型、途中は直線的な幅の変化です。
階段型、10幅・7幅・4幅・7幅の階段状の幅の変化。
2極型、10幅と4幅だけ。
底の平編みだと波模様になりませんが、2つ飛び、3つ飛びの網代編みになると波になる。移動平均みたいなものですから、3つ飛びの方が滑らか。階段状で十分に波となり、幅が2種類しかなかったとしても、ブロック状よりは波に見える。でしょうか。
データです。波型・台形型・階段型・2極型の順。
グラフ元のエクセルもつけておきます。
追記
アプリを使うと、自分で作成した幅と並びから、どんな波模様になるかを見ることができます。操作はこちら。並びの例はこちら。動画もあります。
| 名称 | 波 網代 編み |
| 名称(読み) | なみ あじろ あみ |
| 模様タイプ | 単位の繰り返し |
| 単位 | バンド幅のセットに対して、 6 × 6 [3つ飛び] / 4 × 4 [2つ飛び] で編む |
| バンド幅 | 段階的に広→狭→広→狭 |
| 色 | |
| 飛び数 | 2もしくは3 |
| 対称性 | |
| 備考 |
CraftBandSquare では、それぞれのひもの幅を個別に設定することができます。
3つ飛びで、波網代編みで作ってみましょう。
では、波網代編みのひも幅、狭→広→狭、と繰り返せばよいのでしょうけれど、その刻みはどうしたらよいのでしょうか。
単純に考えつくのは、線形とサインカーブ。12本幅、7点を1セットとして、
で試してみました。
3つ飛びの網代編み、ひも幅以外は同じ編み方です。比較してみると、台形よりは波型の方が曲率が大きいような気がする、、けど、あまり変わらない、、ようにも思えます。
どちらも変わらないのであれば、台形の方が、ひもを効率的に使えます。12本幅を、8-4, 5-7 として使えますから。
ちなみに、ひも幅の差、グラフで比較するとこんなです。
2個を重ねてみました。さて、どちらが台形でどちらが波型か、わかりますか？
台形のデータです。
波型のデータです。
エクセルのデータもつけておきます。
| 名称 | 網代 編み 片流れ 網代 編み 3つ飛び 網代 編み 3本飛び 網代 編み 3本飛ばし 網代 編み 三間 網代 編み 三目 網代 編み |
| 名称(読み) | あじろ あみ かたながれ あじろ あみ みっつとび あじろ あみ さんぼんとび あじろ あみ さんぼんとばし あじろ あみ みま あじろ あみ さんもく あじろ あみ |
| 模様タイプ | 単位の繰り返し |
| 単位 | 6 × 6 |
| バンド幅 | |
| 色 | |
| 飛び数 | 3 |
| 対称軸 | 半回転 |
| 備考 | 右上がり、左上がり |
PPバンドでは、そのままでは3つ飛びは難しいことがわかりましたので、クラフトバンド/紙バンドで3つ飛び 網代編みのボックスを作ってみました。
12本幅を半分に割いて6本幅にしました。2つ飛び網代編みの場合は、霧吹きで柔らかくしないと組むことができませんでしたが、3つ飛びでは、そのまま組むことができました。底・側面すべて3つ飛び網代編みです。
底はこんなです。
斜めとなる方向については既定値のまま、底は左上が開始点・側面は左下が開始点です。底と側面が交差する4辺について、同じにならないことを確認しただけなので、縦(狭い方)の側面と同じになってしまいましたが、横(広い方)に合わせた方が良かったかもしれません。
CraftBandSquare による展開図・編み図です。
データです。