今まで、四方網代編みは、正方形で縦横中央で反転すればよい、と思って作ってきました。でも、立ち上げ位置を検討する中で、方向があるということに気付きました。
中央が3つ飛びですから、試しに、最小サイズのかごを作ってみました。

右上に注目すると、左側はひもが縦・右側はひもが横になっています。この2つは、かごを回転させたとしても入れ替わることはありません。交色でなくても、です。
上の二つのかごをそのままひっくりかえしてみました。反対の面、つまりかごの底を覗くように見ても、ひもの縦横は変わりません。最初にどちらかで編み始めたら、後からは変えられないということです。

先の文献
『かごと器の技法がわかる 竹細工 増補改訂版』田中瑞波、メイツ出版、2023
「PART5 ステップアップする竹かごづくり」78ページから、四方網代編みの底編みの手順が掲載されています。竹ひごの組み合わせ方は、上の写真の左側のタイプです。
どちらも同じではなく、「正式な四方網代編み」であるためには、左側のように編まなくてはいけないのでしょうか。私にはわかりませんが、四つ畳み編みでは両方が共存していましたので、同様に、どちらもあり、ということにしましょう。
そしてもうひとつ。「縦横中央で反転」ですが、次のようなパターンがあり得ます。
3つ飛びですから、中央部は 3・2・1 にすることが出来るのです。

これについては、まだまだ短い経験ではありますが、1や2で作られた例を見たことがありませんので、中央部の四角数3のもののみを四方網代編みと呼ぶ、ということでよいのではないかと思います。
「中央部の四角数3」という条件ですが、これにより、ひもの数から立ち上げ位置が決まります。正方形ですから、縦ひも数=横ひも数であり、辺となる縦横の四角数はひも数の半分です。
底を4分割した左上部分を図示してみました。
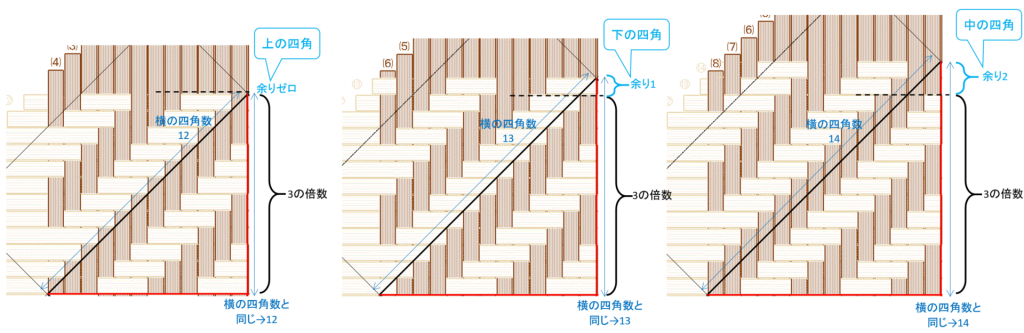
つまり、立ち上げ位置となるのは、
- 辺の四角数を3で割った余りがゼロの時は、上の四角
- 辺の四角数を3で割った余りが1の時は、下の四角
- 辺の四角数を3で割った余りが2の時は、中の四角
上述の文献『竹細工 増補改訂版』によると、立ち上げ位置の角が3本になっていると曲げやすいとのことです。作例は19で、「辺の四角数を3で割った余りが1」となる数が該当します。
上の写真、[ひも上下]の[上下交換]で簡単に入れ替えられますが、2点のデータをつけておきます。色も写真に合わせていますが、縦横は回転すれば同じですので。