「はまぐりの数学」というサイトがあります。「社会や自然と数学のつながりを探る」というコンセプトのもと、自然や生物、身の回りの事象など様々なテーマについて、代数・解析・幾何といった数学的手法に加え、目に見える・触れる現物を作ることで、生徒にもわかりやすく優しく説明されています。
中の「籠目(カゴメ)編みとフラーレン」というページでは、六つ目（籠目）編みを使って、四面体・八面体・十二面体・二十面体、さらには凹凸や穴のある立体まで、様々な立体を実際に編んで作りながら分析されています。

鉄線編みのかごを試作していて、よくできた編み方だなぁと思うと同時に、どんな仕組みでできているのだろうと思うようになりました。そこで、はまぐりの先生に、鉄線編みについても、数学的な見地から分析していただけませんか、とお尋ねしてみました。

籠目編みとの関連性はすぐにご理解いただき、早速、とりかかっていただけることになりました。「かご」で普通に思い浮かぶのは直方体ですから、まず検討されたのが四角い かご、いわゆる「六つ目四角かご」です。それがこちらのページです。

「籠目編みで正八面体を作る」～オイラーの多面体定理の応用における理論と実践～

ここから「六つ目四角かご」の底の立ち上げ方について、結果のみを取り出してみました。

まず、普通の六つ目のかご。3方向に組んだ六角形の底を、ひごに平行に、六角形に立ち上げます。すると、立ち上げた各角、六ヶ所に五角形が作られます。この五角形を「⑤」として図示しました。左右は同じですので、左側半分だけマークしています。

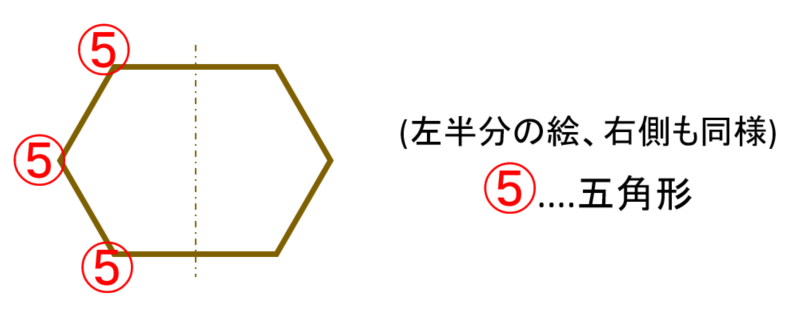
「六つ目四角かご」は、四角底ですから、底には四か所の角が作られればよい。そのためには、角を二つ(片側につきひとつ)減らす。それには五角形と七角形を組み合わせる。理論上の条件は、

(五角形の数) － (七角形の数)　＝　６　(片側については3・六角形はノーカウント)

下図、縦のひごはそのままとし、横のひごで調整する例です。
左側が最小で横のひご4本。ひごは、2本ずつ増やすことができますので、6本、8本と増やした例を並べました。( 同様に、⑤が五角形、⑦が七角形です)

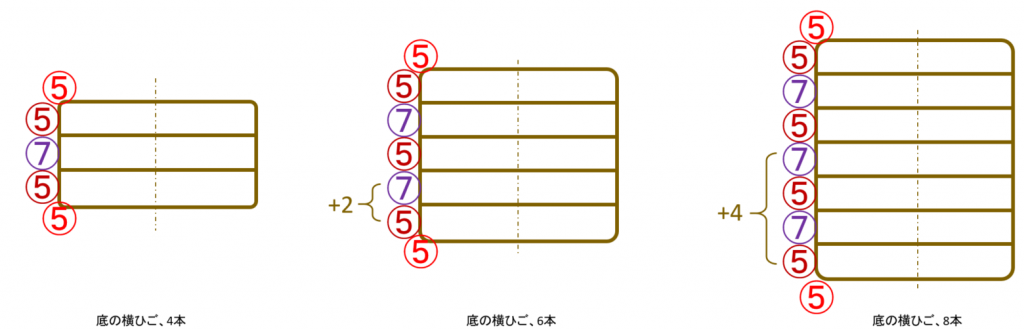
この数で五角形と七角形を組み合わせれば、六角形の底を四角形にできるのです。上述のページでは、PPバンドで実際に立体を作って、可能であることを実証されています。

四角の底のかごは、六角形に立ち上げるかごとは違う作り方をする別もののように思っていたのですが、この結果を見て、多角形の組み合わせであり地続きだということがわかりました。

数学ってすごい。はまぐりの先生、ありがとうございました。