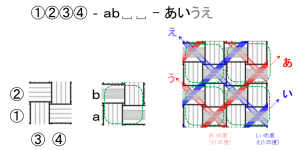
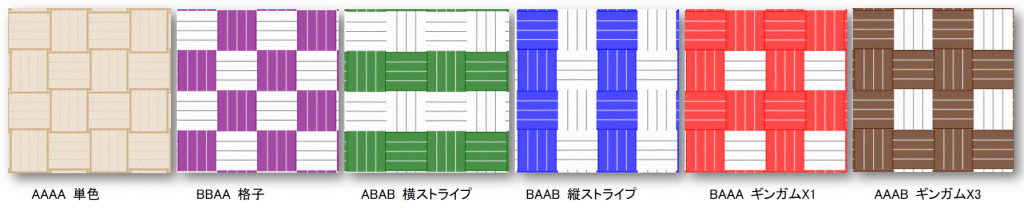
最初のレベル2ステッチ「クロス模様」では、以下の幅のバンドを使用しています。
なぜこの組み合わせになったのか、その理由を当時の背景とともに紐解いてみましょう。
まず、土台となる「レベル1」についてです。既に持ち手などに1/2幅のバンドが使われていましたから、レベル1に同じ1/2幅を採用するのは自然な流れでした。
次に、そこに重ねる「レベル2」がなぜ1/4幅なのかという点です。これにはスペースと道具という2つの理由があります。
物理的なスペースの問題として、1/2幅で埋まっている場所に、斜め方向からさらに同じ1/2幅を通す余裕はありません。必然的に、それよりも細いバンドが必要になります。
そしてもう一つは、2014年当時の道具の事情です。 当時はハサミや自作の道具でカットしていたため、正確に3等分(1/3幅)にするのは難しかったでしょう。一方で、バンドを半分に折ってカットするのは簡単です。つまり、1/2幅をさらに半分にした1/4幅を作るのが、手作業において最も合理的で確実な方法だったのです。
しかし、現在は状況が異なります。 2023年から2024年にかけて、PPバンドを簡単に等幅に割ける、PPバンドカッターなどと呼ばれる専用ツールが発売されたからです。これにより、以前は難しかった「1/2幅」「1/3幅」「1/4幅」といった細かい調整も、誰もが手軽に行えるようになりました。
では、道具の進化により「1/3幅」という選択肢が加わった現在、実際にどのような組み合わせが可能なのでしょうか。
まずは、数値的な側面から検証してみましょう。 15mm幅のPPバンドを使用した場合、ベースとなる「押さえのひも(レベル1)」と、斜めに通す「クロスひも(レベル2)」の間に、どれくらいのスペースがあるかを計算したのが下の図です。
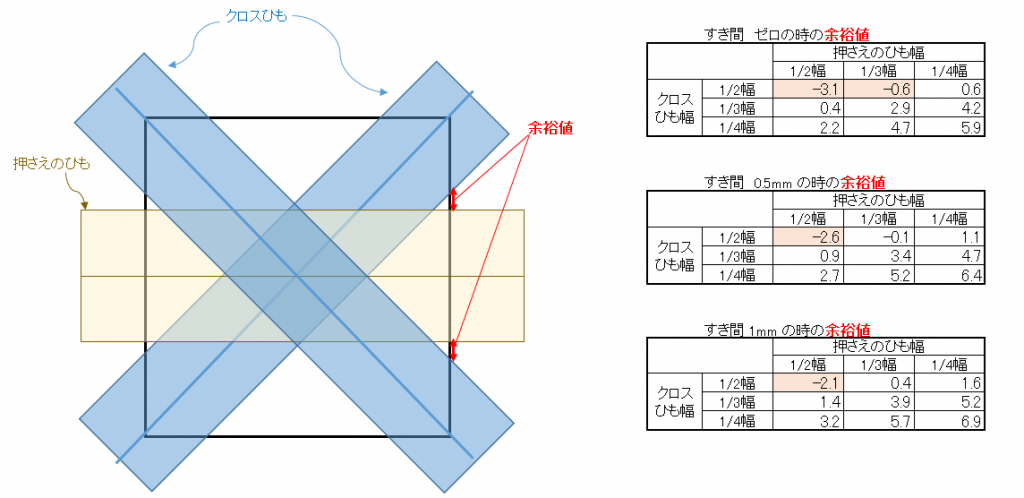 クロスにバンドを通す時のひも幅ごとの余裕値
クロスにバンドを通す時のひも幅ごとの余裕値
表の数値は、バンド同士の「余裕値」を示しています。これがマイナスになっている箇所は、物理的にスペースが足りずひもが重なる、つまり通らないことを意味します。プラスであっても、小さければ通しにくい。また、大きすぎる場合は可動領域が広い、つまりずれやすいことを意味します。
この数値だけではイメージしづらいかもしれませんので、バンド間のすき間を0.5mmに設定した状態を、図で可視化してみましょう。
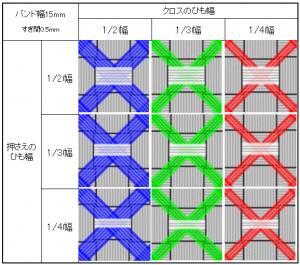 すき間値を0.5mmとしたとき、クロスと押さえのバンドの図
すき間値を0.5mmとしたとき、クロスと押さえのバンドの図
「1/2幅」のベースに対して、「1/4幅」は通しやすくずれにくい絶妙な値です(上段・右列)。でも同じ「1/2幅」をクロスさせようとすると、大きく重なってしまい通すことができません(上段・左列)。
一方で、これまで難しかった「1/3幅」であれば、1/2幅のベースに対してもなんとか通すことができます。さらに、「1/3幅 × 1/3幅」同士の組み合わせ(中段・中央列)であれば、従来の「1/2幅 × 1/4幅」と同じような感覚で、無理なく通せることがわかります。
では、実際に作品にした場合、見た目はどう変わるのでしょうか?
最もポピュラーな「花模様」を例に、3つのパターンを比較してみます。

左から順に以下の組み合わせです。
- 左:1/2幅 × 1/4幅(従来の基本スタイル)
- 中:1/3幅 × 1/3幅(均等なバランス。柔らかな印象)
- 右:1/4幅 × 1/2幅(クロスを太くした逆パターン。明確な分離)
※画像ではレベルごと同じ幅にしていますが、色ごとに幅を変えればさらに表情が変わります。
長らく「1/2幅 × 1/4幅」が基本とされてきましたが、それは絶対的なルールではありません。 道具が進化し、選択肢が増えた今、作りたい模様の雰囲気や好みに合わせて、ひも幅の組み合わせも選べるのではないでしょうか。