長方形のかごを作るのに、斜め網代編みの底といえば、長桝網代編みでした。本やネットの情報を探しても、示されている編み図は、基本的には長桝網代編みですし、(推測ですが)教わるとしたら長桝網代編みのやり方でしょう。
では、普通の二つ飛びや三つ飛びの網代編みを、そのまま底にしようとした人は、いないのでしょうか。やってみたけれどダメだったのか、そもそも最初から、斜め網代の底編みはこうですよ、という常識があったから考えたこともなかったのか。
思い起こすと、私もやったことはない。できなさそうだし、作るのは大変だし。
でも、CraftBandSquare45のデータ上でなら、簡単に試すことができます。今更ですが、やってみました。
連続した「三つ飛び網代編み」
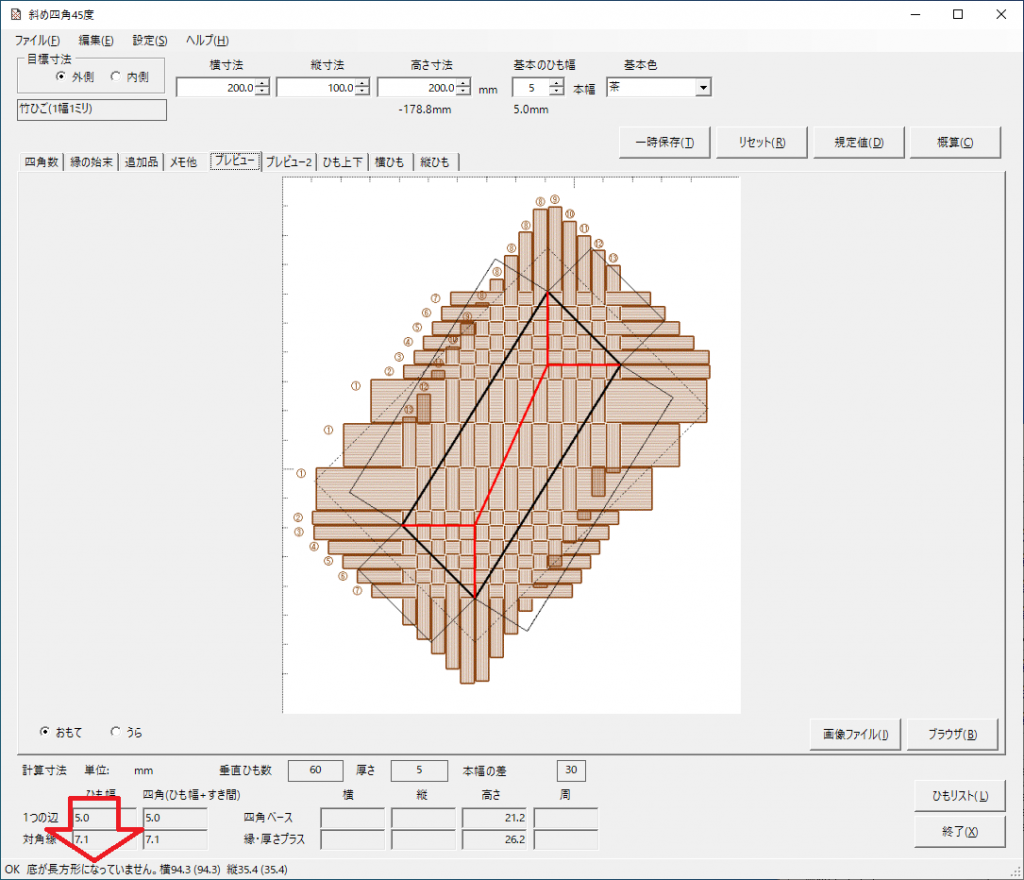
横の四角数 13、縦の四角数7、高さの四角数5にしてみました。あまり大きくなく、倍数関係でない値。
[ひも上下]のタブで、「開始高さ」をゼロにして編み目を表示させ、[設定呼出]ボタンから「6×6-33-網代編み3つ飛び」を選んで[OK]とします。「1回のみ」のチェックはオフ(初期値)のままです。これで、全面に「三つ飛び網代編み」の編み目を繰り返し適用できます。
[プレビュー]の底編み図です。底部分だけですが、シンプルな三つ飛びです。

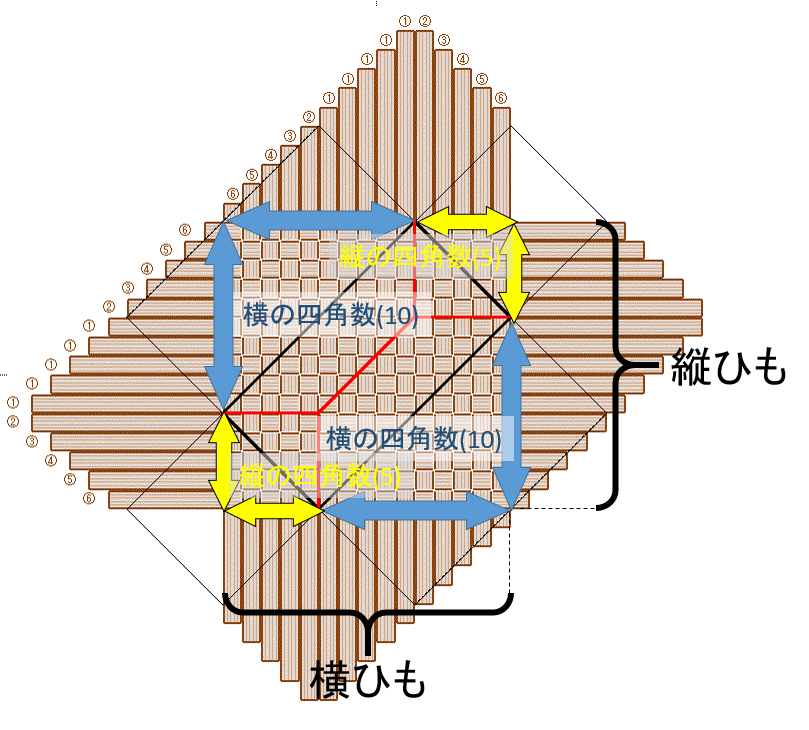
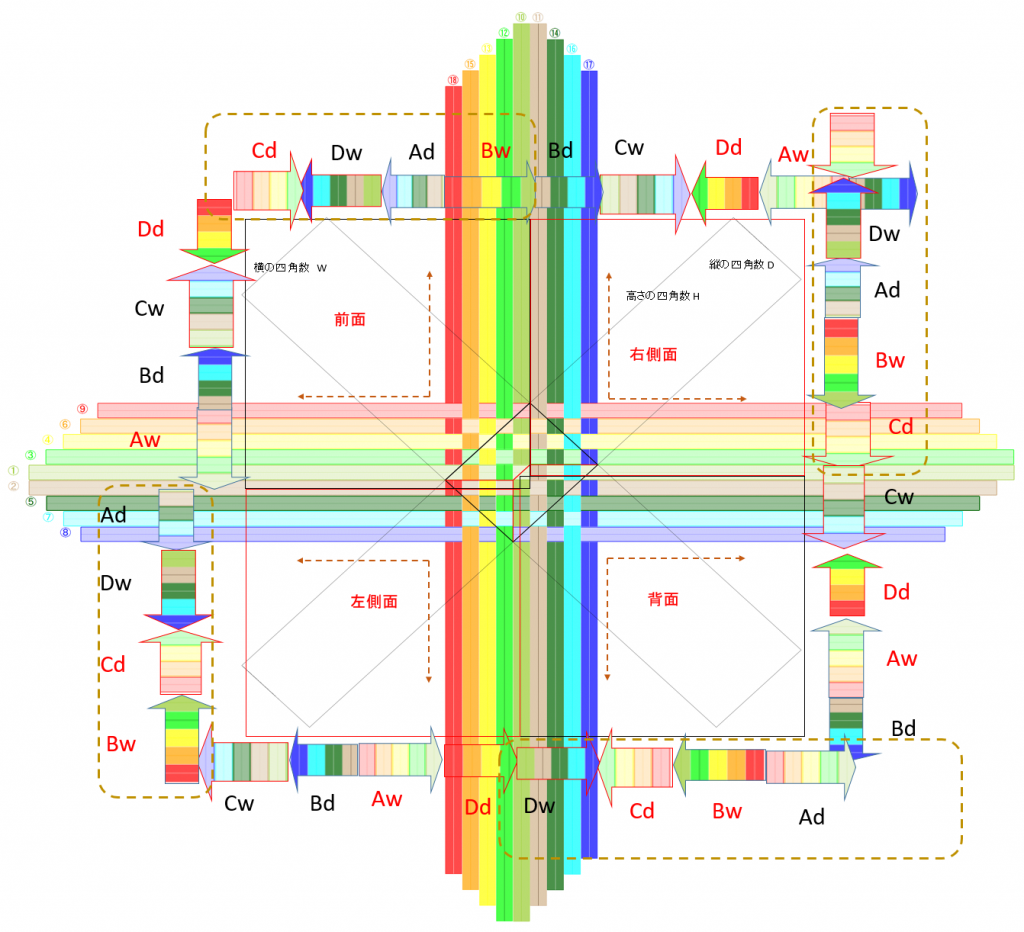
[プレビュー2]では、全面を編んだ時の画像を見ることができます。うち、実際には《編めない》箇所を赤丸で囲ってみました。底は一続きですから編めますが、側面の辺は、両側面のひもが続いていないと編めません。ひも方向の線が不連続になっていたらNGです。
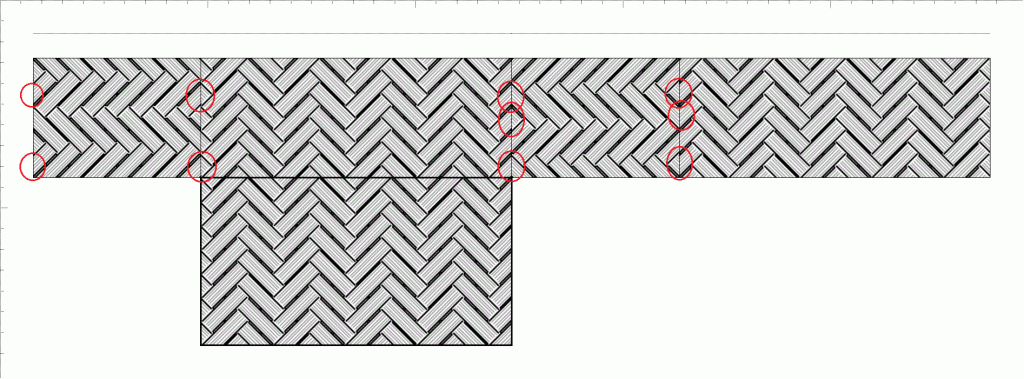
三つ飛びの流れの方向は、隣り合う側面で90度、異なります。側面が続かないのは、素数だからではなく、縦と横が接しているからのようです。実際、編みかえ網代編みの境界線には、3だけではなく1,5が出てきますから。
つまり、三つ飛びを続けようとしても、立ち上げた後の側面が、そのままでは編めないということが確認できたわけです。
「三つ飛び網代編み」のパッチ
テストついでに、ムリヤリ編めるようにしてみましょう。
上のデータの[ひも上下]のタブで「開始高さ」を高さの四角数5に合わせます。編集サイズの「水平に」「垂直に」をともに30とし[サイズ変更]ボタンをクリックします。30というのは、全体の編み目を作るためのサイズで、以下の計算結果です。
<横の四角数> + <縦の四角数> + 2*<高さの四角数>
これで、底編集状態になります。
[設定呼出]ボタンから「上下図の呼出」画面を開き、上下図名は先と同じ「6×6-33-網代編み3つ飛び」ですが、こんどは反映方法の「入れ換え」のチェックをオフにし「繰り返す」にチェックを入れて[OK]とします。
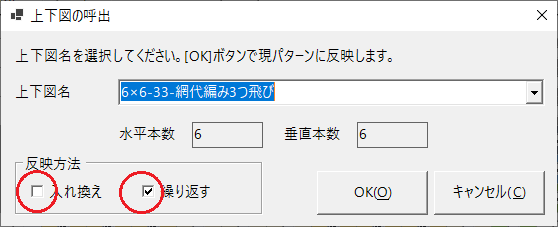
この操作で、全体の編み目が「三つ飛び網代編み」になります。[プレビュー2]で表示させると、今の場合、繰り返し時と同じ画像を見ることができます。
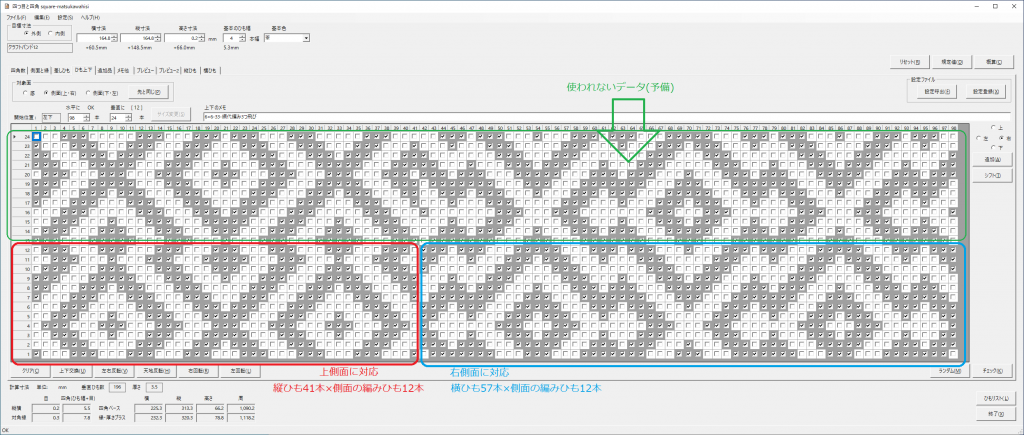
《編めない》箇所は、右下にある[側面確認]ボタンをクリックするとチェックすることができます。今のデータの場合、次のようなメッセージが表示されます。
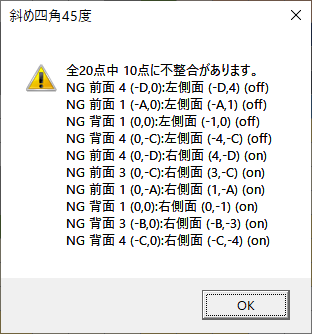
この後表示される「チェック結果を反映させますか?」の問い合わせに対して[はい]とすれば、前面・背面側の状態に整合できます。側面の辺の不整合がなくなり、編めるようになるわけです。
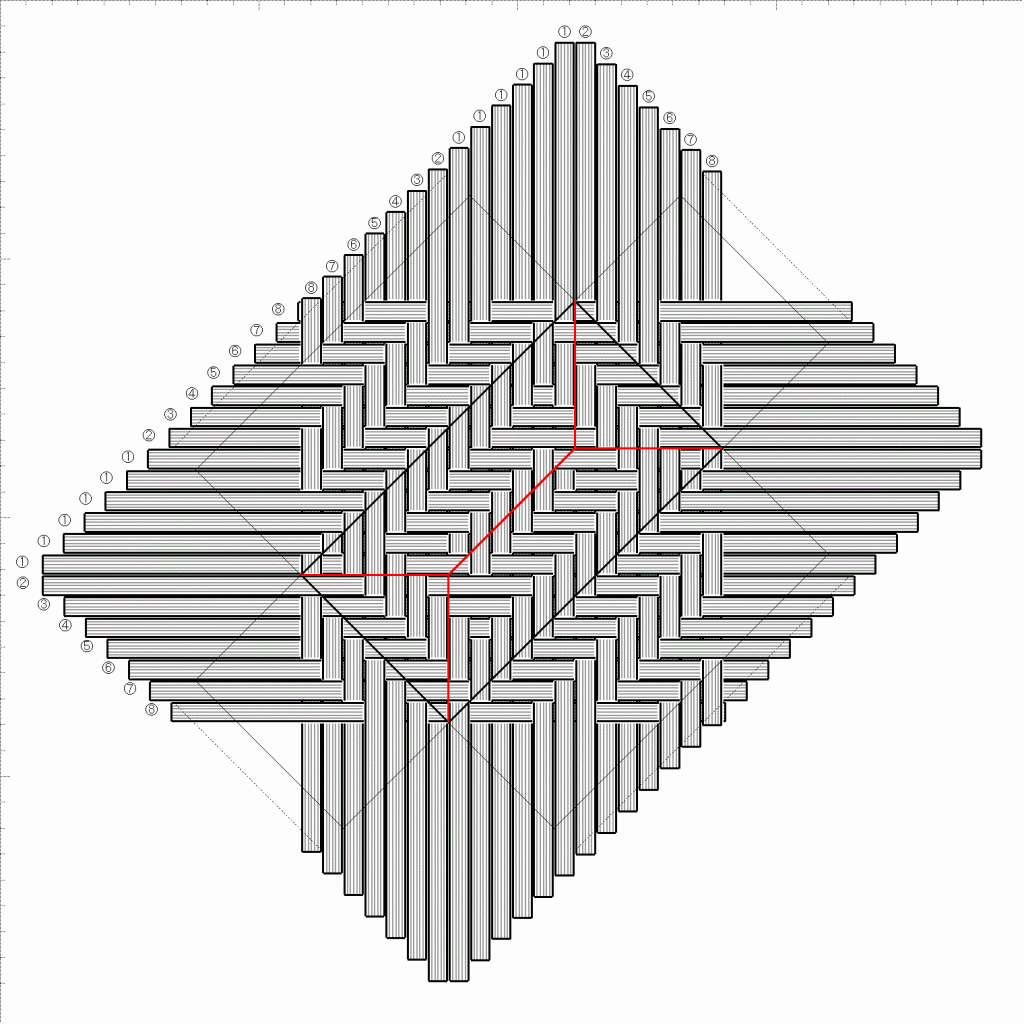
修正後の[プレビュー2]画像を見てみましょう。

機械的に合わせただけで、編みやすさや飛び数は考慮されていませんが、編めるようにはなったはず。先の図と、問題個所を比較してみてください。
長桝網代編み
同じサイズとひも数で、長桝網代編みも作ってみました。
[ひも上下]で、「開始高さ」には、高さの四角数と同じ5、「垂直に」には1、「底に」には2とし、[合わせる]とします。(「垂直に」「底に」は、早見表で「縦の四角数」7の3で割った余り1を参照した値です。その後、手順に従って修正します)
[プレビュー]で見ると、底は入れ子の長方形です。
側面は、横方向に揃います。