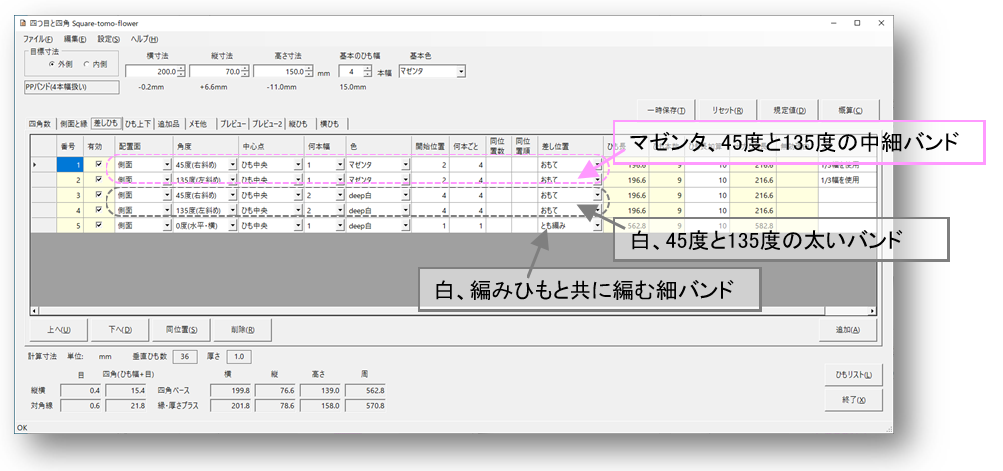
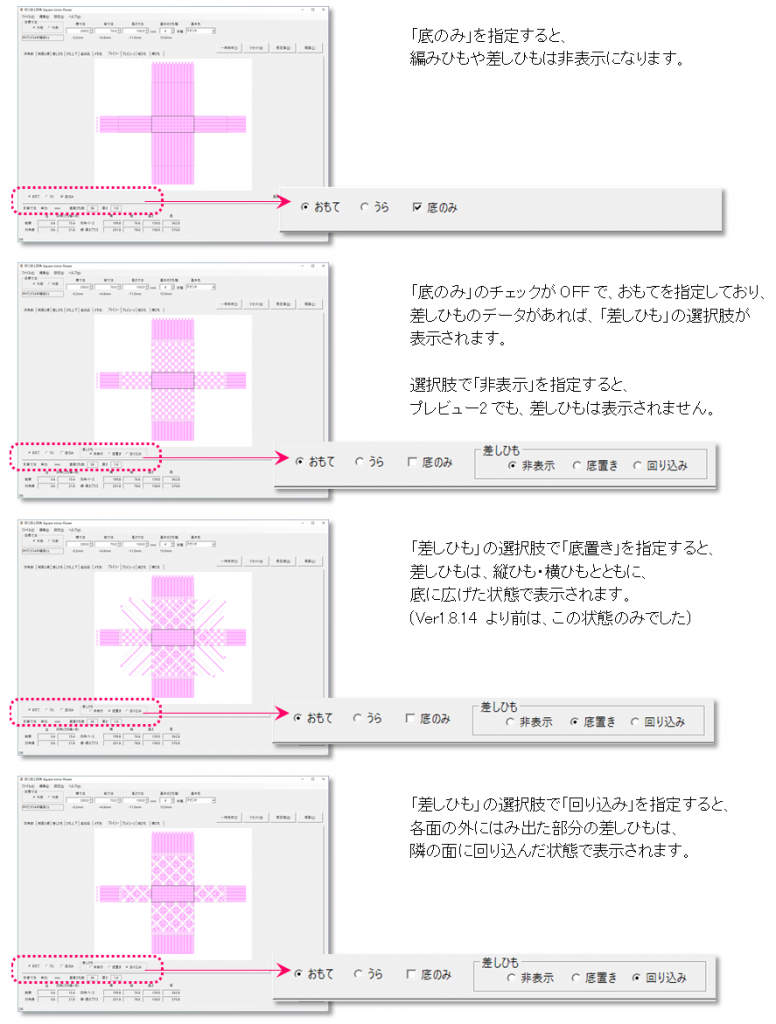
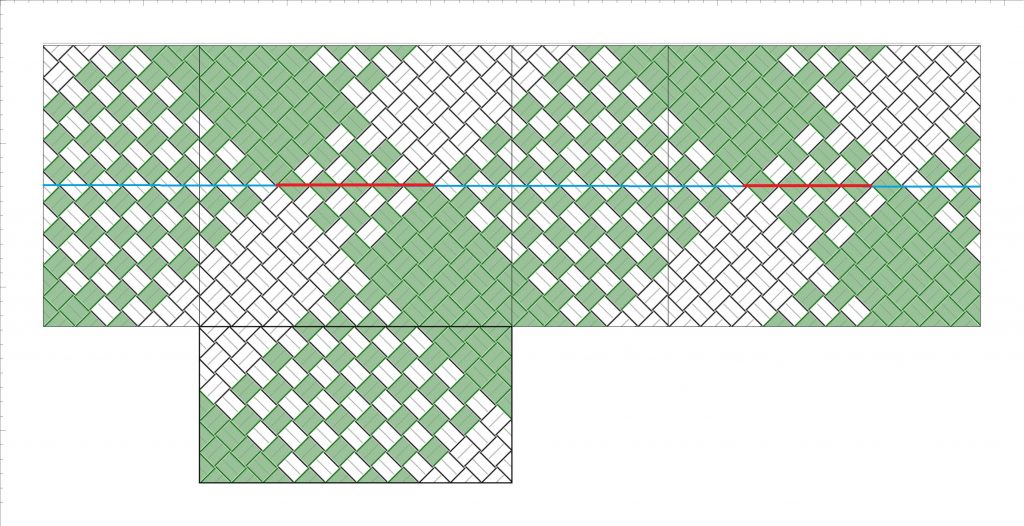
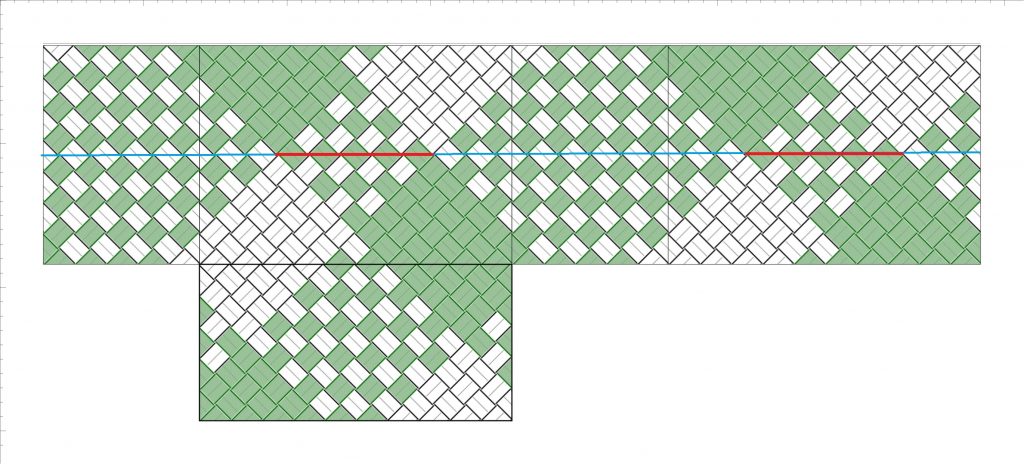
ここまで何点か「折りカラー編み」のかごを作ってきましたが、改めて、折りカラー編みとは何なのでしょう。ひとことで言うと、こうです。
「バンドを折り返したときに現れる色を活かして 模様を作る編み方」
この編み方の特徴は、裏表が同色のバンドを使用することにあります。折り返したバンドの裏面も、表面と変わらずに使うことができるため、意図的に模様の一部として取り入れることが可能になります。
従来、かごを編む際の模様づくりでは、主に表側のデザインのみが考慮されてきました。また、カットされたバンドの端は「縁」として処理する必要があり、折り返して処理する場合は、デザインに影響を与えないよう、次のような方法が取られてきました。
折りカラー編みでは、この折り返し部分をデザインの一部として活かし、新たな模様を生み出します。
- 折り返しによって、バンドの裏面を別の色のバンドに重ねることができる
- 重ね方を工夫することで、色を変えることも、もとの色を残すことも選べる
このように、最初に作られた模様に「折り返し色」が加わることで、独自のデザインが完成するのが折りカラー編みの特徴です。
さらに、折りカラー編みでは、後から短いバンドを差し色として重ねるのではなく、底から伸びたバンドをそのまま使うため、強度が増し、縁の一体感が生まれます。
適用例
折りカラー編みの一番シンプルな適用例が、縦横二色の斜め編みです。すなわち、縦A色・横B色の二色で底を編み、斜め45度方向に折って立ち上げるパターンです。
底はA色とB色のクロスになっていますが、立ち上げた側面はクロスが崩れます。A色とB色が斜めに組み合わさり、A色B色のクロスだけでなく、A色同士・B色同士のブロック箇所が現れるのです。
折りカラー編みで、特定の高さで縁を作り、一部を外側(表側)に折り返すことで、A色同士・B色同士のブロックをクロスに戻し、外側の側面全体をクロス状態にすることができます。
更に、残り部分を内側(裏側)に折り返すことで、内側の側面もクロス状態にすることができます。そして、外側・内側の両面を折り返せば、側面全体が二重になった編地が作られます。
具体例で見てみましょう。
縁での折り返し
 縁の折り返しタイプ
縁の折り返しタイプ
交差する2本が同色の場合(左図)は折り返しても色は変わりませんが、異なる2色が交差する場合は、色を変える(中図)ことも保持する(右図)こともできます。
斜め立ち上げと側面のバンド色
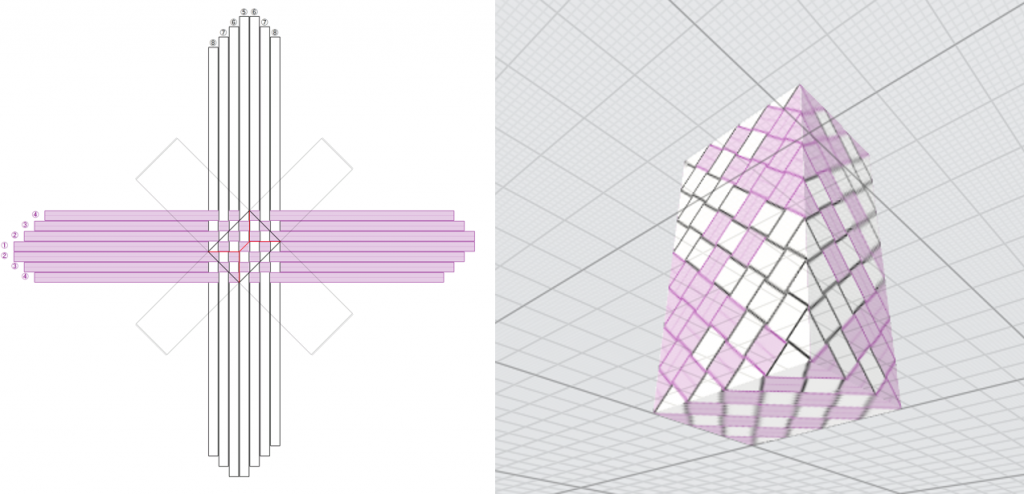
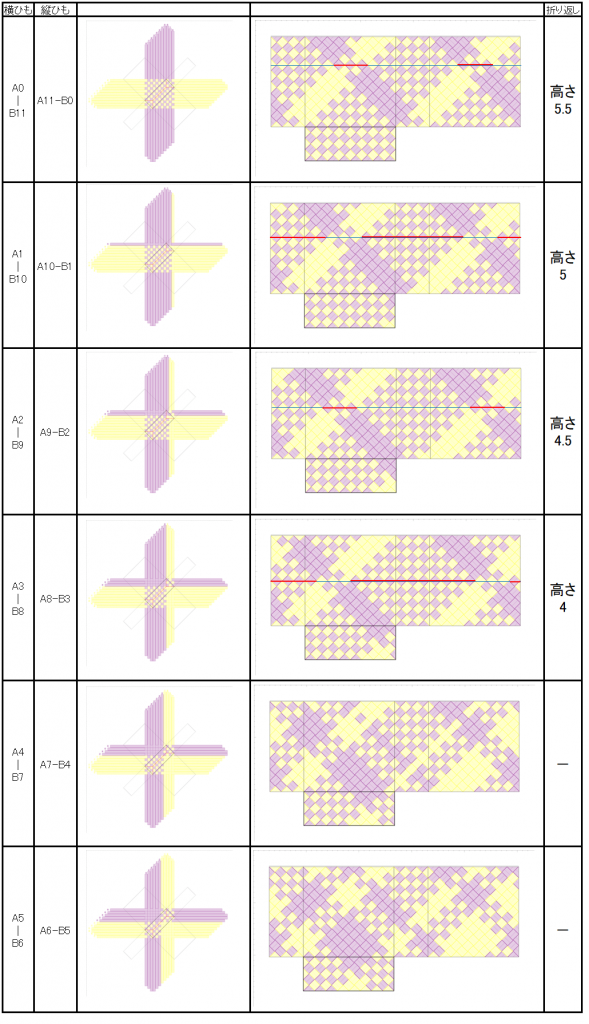
縦のバンドが白、横のバンドが紫で、平編みの例です。左図のように底を作り、黒枠線で示した位置を底として立ち上げて側面を編むと、右図のようになります。底はクロス(格子模様)ですが、側面には同色のブロックが現れます。
全バンドが交差する高さ位置
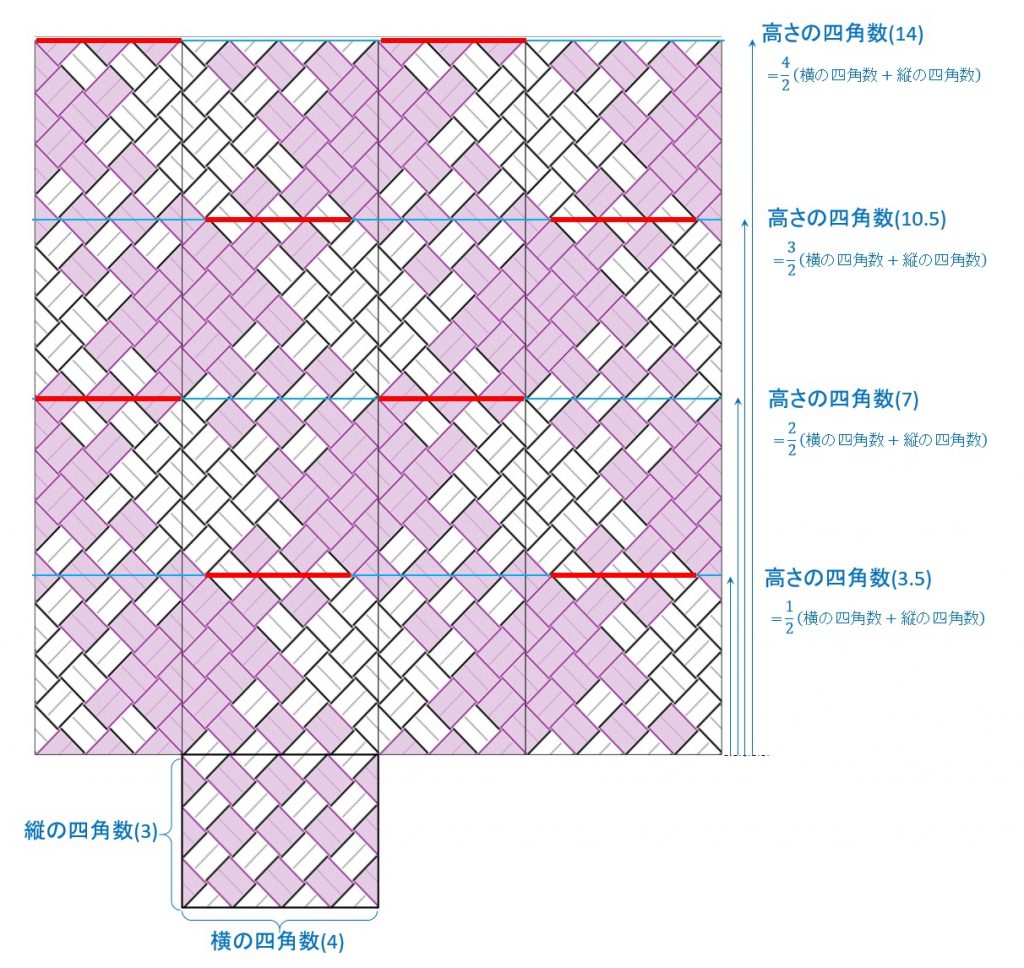
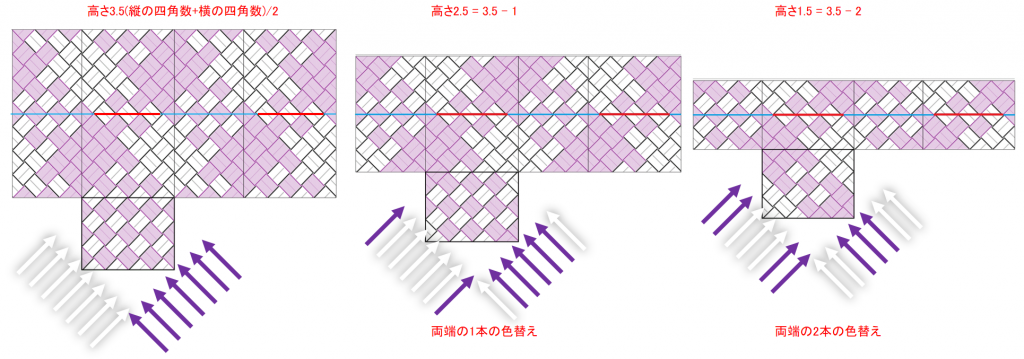
底を縦と横、別の2色のクロス(格子模様)にした場合、交差したバンドで作られる四角形を単位とすると、側面の高さが
(横の四角数 + 縦の四角数) / 2
の定数倍の位置では、全てのバンドが2色の交差状態になります。
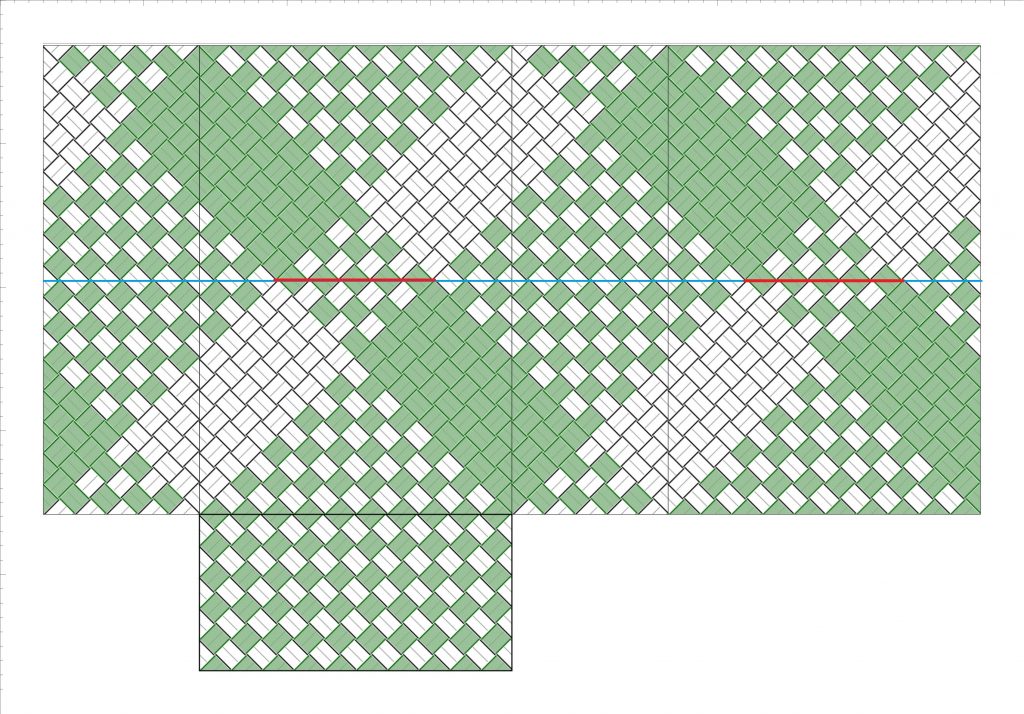
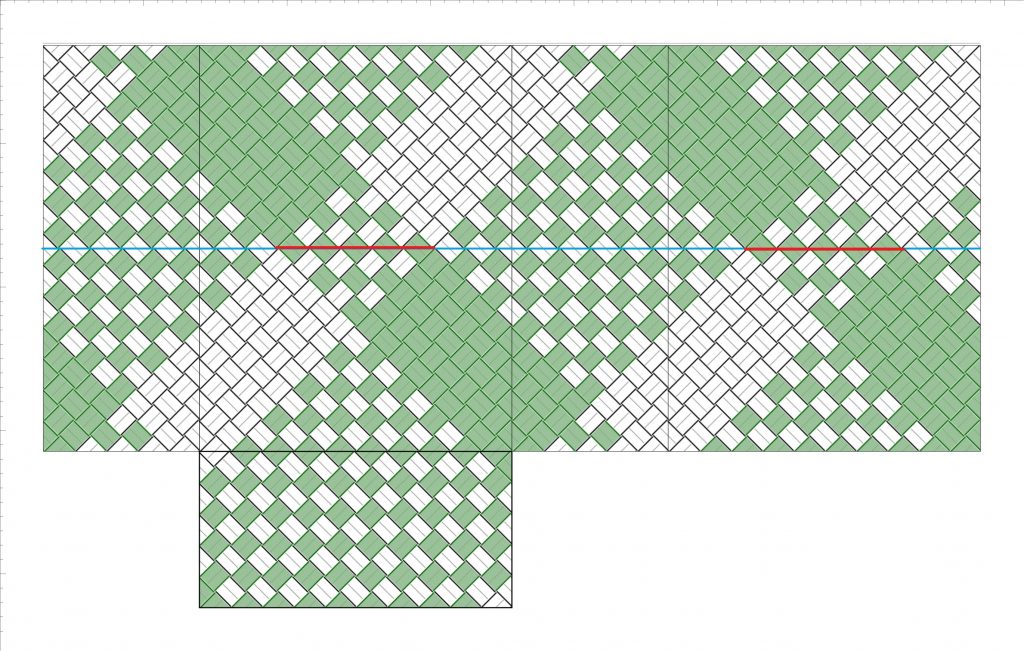
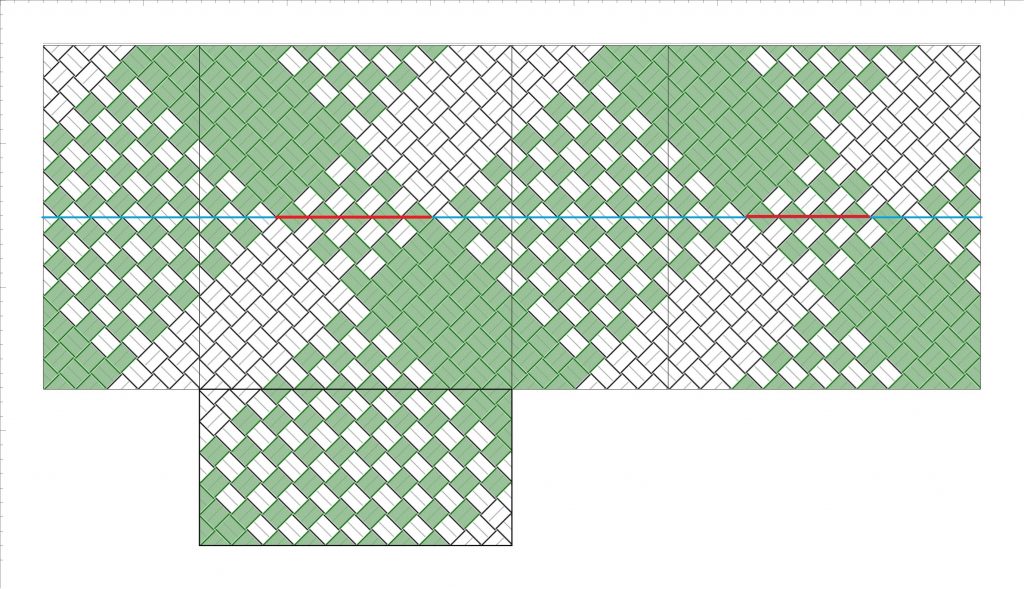
上図は、横の四角数4・縦の四角数3で平編みした時の展開図です。上の式に該当する高さの四角数、3.5・7・10.5・14 を例示しています。
折りカラー編み
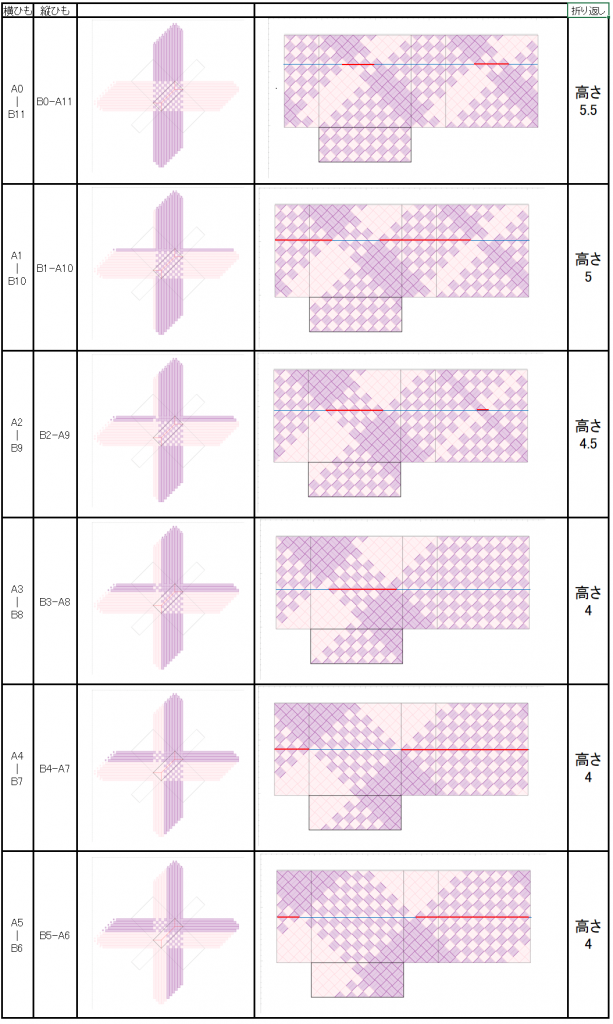
全バンドが交差する高さ位置を縁にすると、折り返す時に、全バンドに対して、編み色を変えるかどうかを選ぶことができます。表側(外側)の模様についてであれば、
- 色を変えるのであれば、外側に折り返す
- 色を変えないのであれば、内側に折り返す
とすればよいのです。
そして、上図4つの縁のライン、各、赤線と青線で示した部分(=クロス領域の対角線)は、同色ブロックの切り替わり箇所でもあります。なので、このライン上で、赤線ラインもしくは青線ラインのいずれかを外側に折り返せば、側面全てを2色のクロス(格子模様)に戻すことができます。
更に、裏側(内側)についても同じ状態になっており、縁は赤線ラインと青線ラインで分離していますから、外側に折り返した残りを内側に折り返すことで、内側も2色のクロス(格子模様)にすることができます。
[※]ただし、原理的に、底と側面の格子をすべて連続させることはできません。どこかで調整が必要ですが、位置は選べるので、それぞれのかごに適した場所にすればよいでしょう。
この例、横の四角数4・縦の四角数3で、小かごを作ってみました。高さの四角数7と3.5の2点です。

外側の方が重ね編みしやすいので、横の四角数4に対応した青線ラインで外側に折り返しました。内側にも折り返したのですが、高さ7の方は底まで手が届きにくく、下の方は妥協してしまいましたが。
CraftBandSquare45 のデータです。各、指定位置で折りカラー編みしてください。