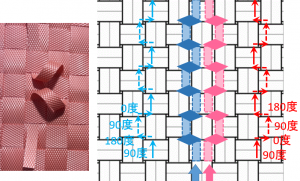
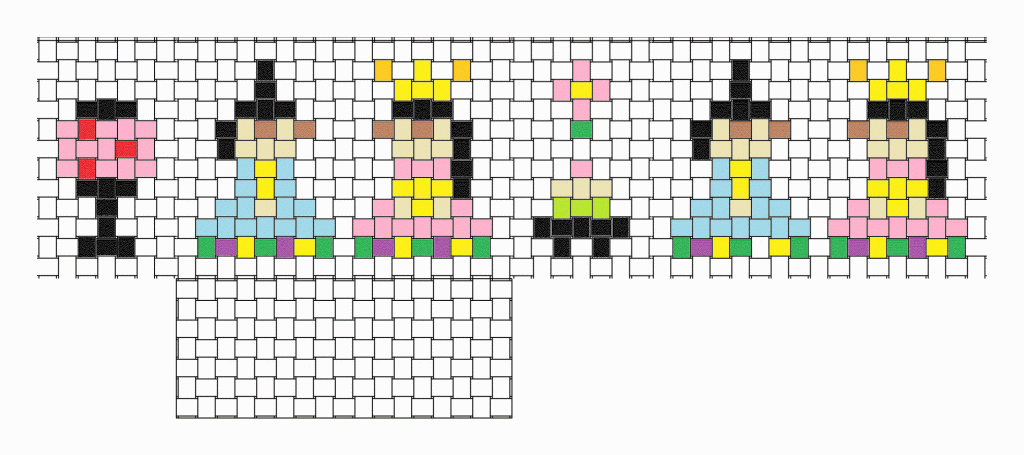| 名称 | 鱗(うろこ)模様 | Scale Pattern |
| 概要 | 1/2幅のループ2個 | AAAA-UAA |
| 単位 | [水平方向] 2 | [垂直方向] 2 |
| レベル0 | [水平] ベース色 | [垂直] ベース色 |
| レベル1 | [垂直] 0: – | 1:ベース色(1/2幅) を並べて2本 1本は、90度→0度→90度→180度 で90度方向に進む もう1本は、90度→180度→90度→0度 で90度方向に進む | |
| レベル2 | ||
| 備考 | 1コマに1/2幅が2本 ループで対角線方向に移動 | 転置 鱗形状の方向 |
富田淳子 (2015). 『PPバンドで作るベトナムのプラカゴ』 文化出版局.
78-79ページ、作品30「うろこ編みのバッグ」からです。
全面がうろこのような立体的な模様になっています。ベースに通す、レベル1のステッチです。

内側には模様はありません。側面に通した後差しひもを、そのまま底に重ねて始末しています。
平編みの目を通すのに、平たく差し込んだのでは通らないところ、ループを作ることで隣の列に移動して通します。持ち手を固定するのに使われる技法です。
1/2幅の後差しひもなので、ベース1コマに2本通ります。それぞれ、右隣と左隣を行き来しつつ、側面を垂直方向に通します。
1単位分の編み目(赤枠・2×2)です。うろこ部分は段にわたっているのですが、うろこ半分の形は編めないので、下から差してその上にうろこが作られる扱いです。右図はプレビュー図ですが、うろこ形は表示できないため、ベースとなる垂直方向のラインを示し、うろこ部分を書き加えました。
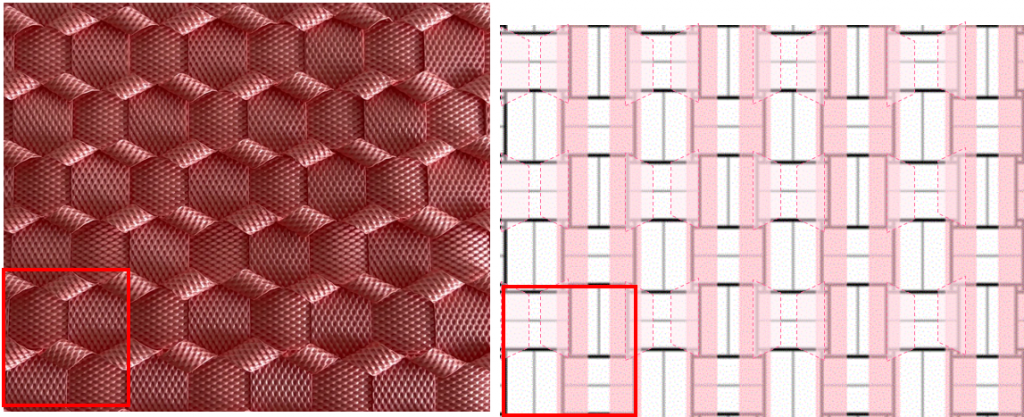
※前側面の左下から、右(0度)方向・上(90度)方向にカウントアップ。左下は垂直方向がover/水平方向がunderです。
Squareのデータです。差しひもについては、ループするため長さの2倍ほどのバンドが必要になります。ひも長加算値には、このかごのサイズに合わせた長さをセットしています。