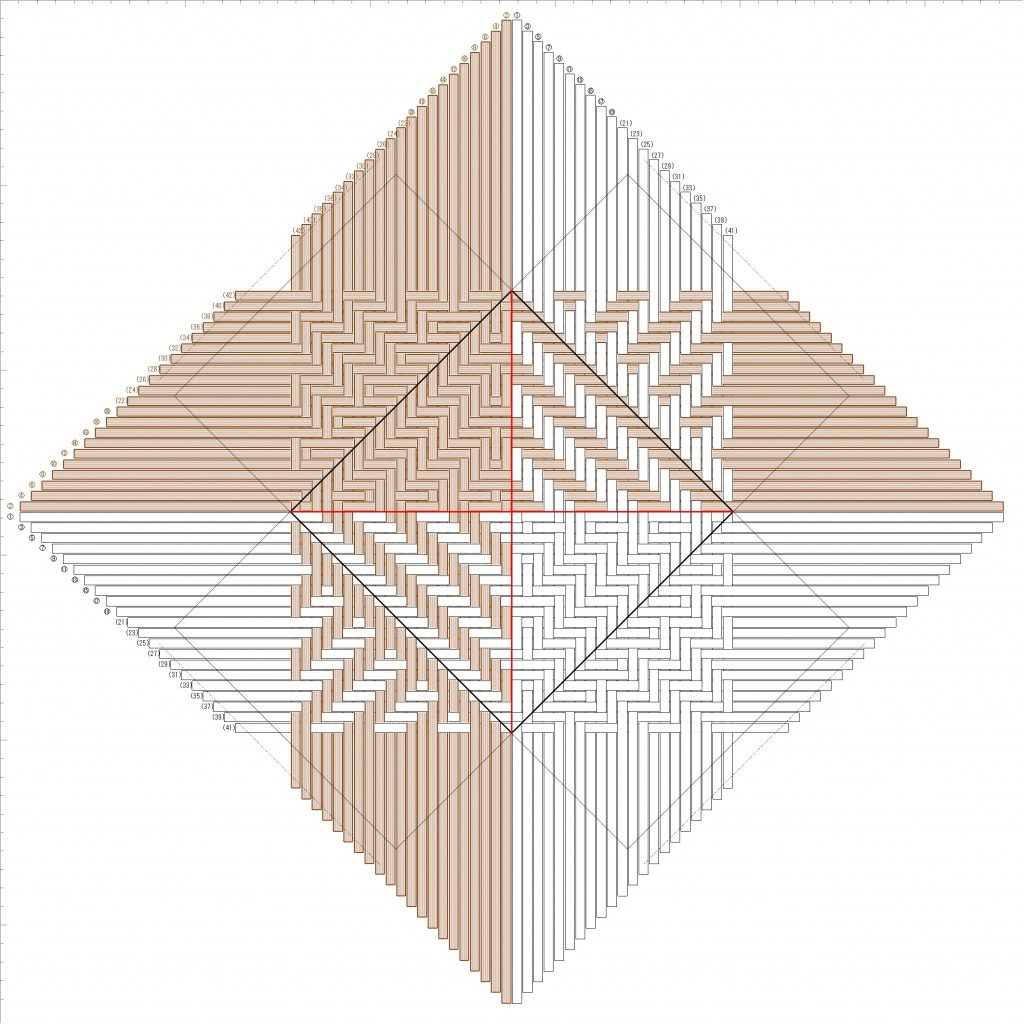
幅と並びを変えた波網代を何点か作ってみましたが、更に編み目を変えるとどうなるでしょうか。先のテスト用フレームで「1,2,3,4,5,6,7,8,9,9,8,7,6,5,4,3,2,1」のパターンで試してみましょう。
[色の繰り返し]画面を次のような値にセットし、[変更実行]とすると、縦ひも・横ひもともに繰り返しが適用されます。プレビュー図を確認後、[横ひも]タブの[リセット]ボタンで、横ひもをすべて5幅にリセットし、先の図と比較してみます。
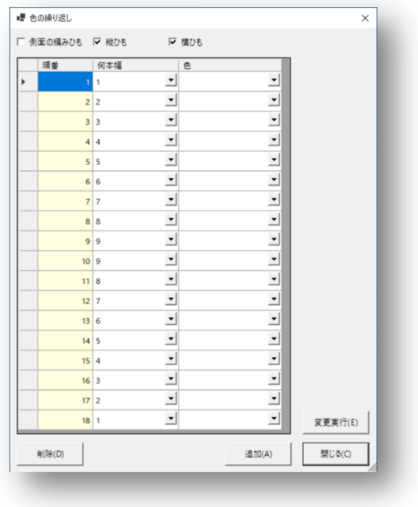
縦ひも・横ひも、ともに18点の繰り返しですので、編み目の単位もこのサイズに合わせましょう。
[ひも上下]タブを開き「水平に」「垂直に」のそれぞれの数値、いずれも18にしてから[サイズ変更]ボタンをクリックしてください。
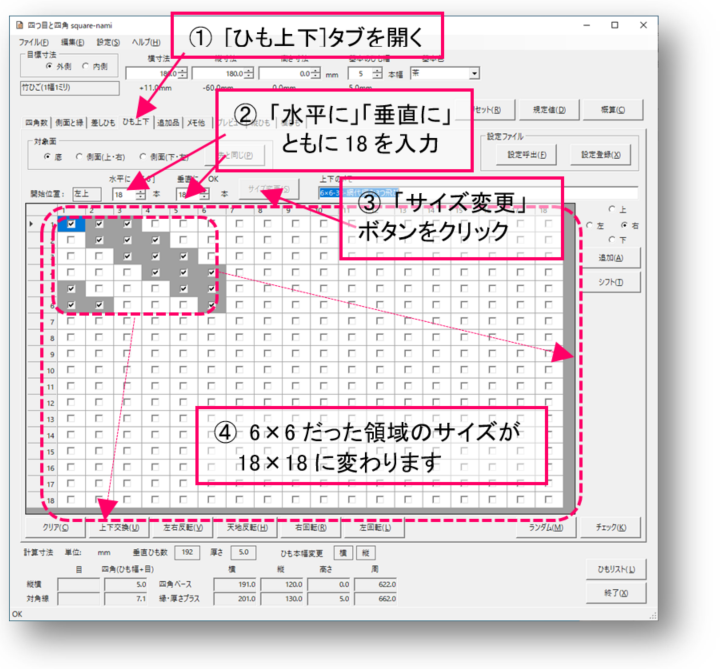
編集領域のサイズが、6×6から18×18に拡大されます。ここを、3つ飛び網代編みで埋めましょう。
[設定呼出]ボタンをクリックして、再度「上下図の呼び出し」画面を表示させます。先と同じ「6×6-33-網代編み3つ飛び」を選択しますが、今度は、反映方法を入れ換えなし、繰り返しあり、にします。
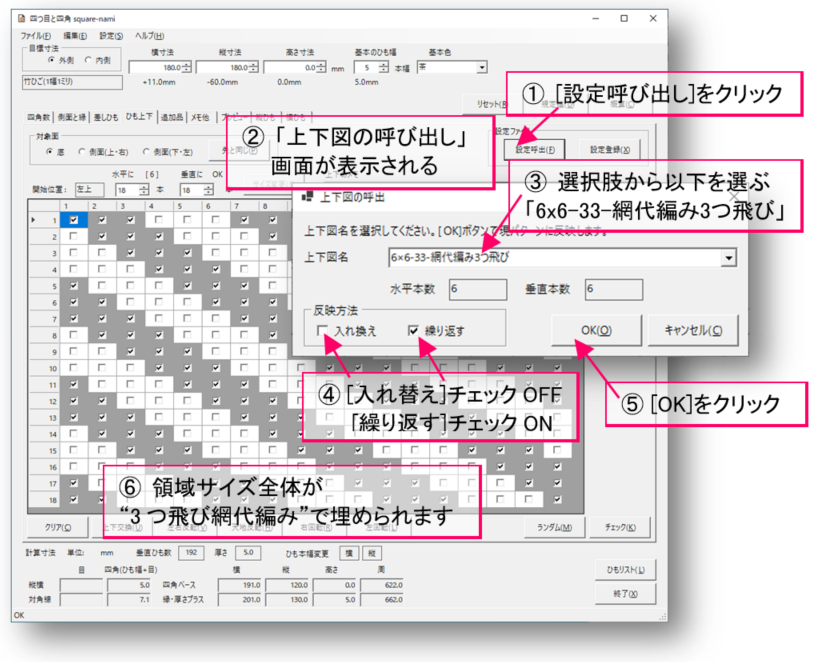
プレビュー図は先と同じになっているはずです。単位サイズは大きくなりましたが、連続した3つ飛び網代編みになっているからです。
次に、この単位の右半分を左右反転してみましょう。18列の半分ですから、10列1行から18列18行の範囲をクリック&ドラッグして選択状態にします。「左右反転」ボタンをクリックすると選択されていた領域が左右反転します。いずれかのセルをクリックして領域選択を解除し、編み目を確認してください。
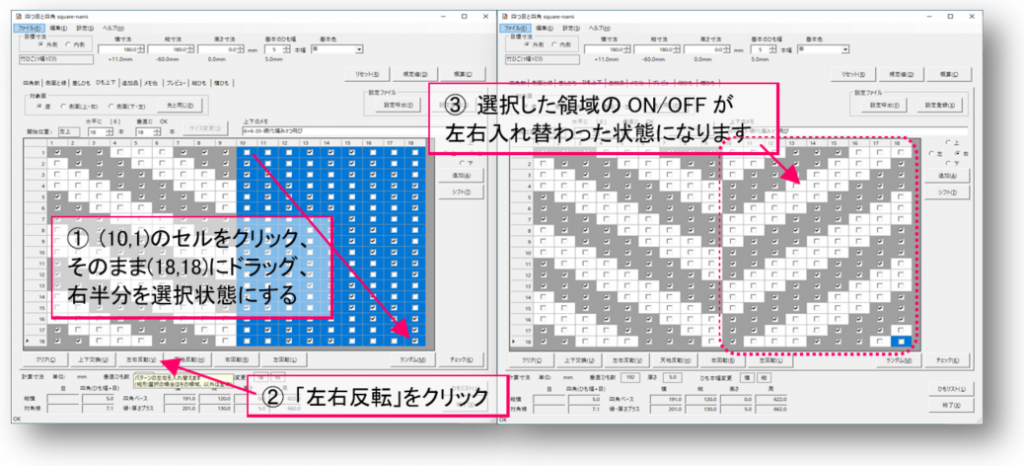
網代編みの流れ方向が9列ごとに反転しました。プレビューで見てみましょう。
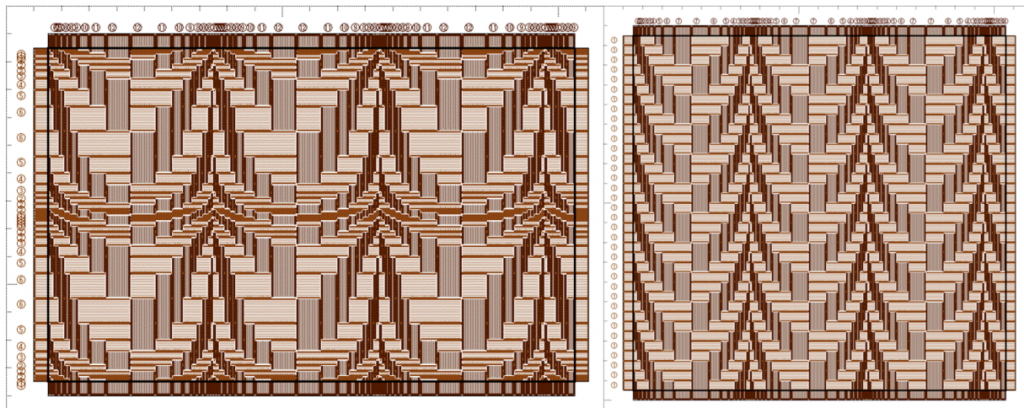
左側は、縦ひも・横ひもとも波網代、右側は横ひもをリセットした縦ひものみ波の図です。
同じ様にして、上半分を「天地反転」しましょう。
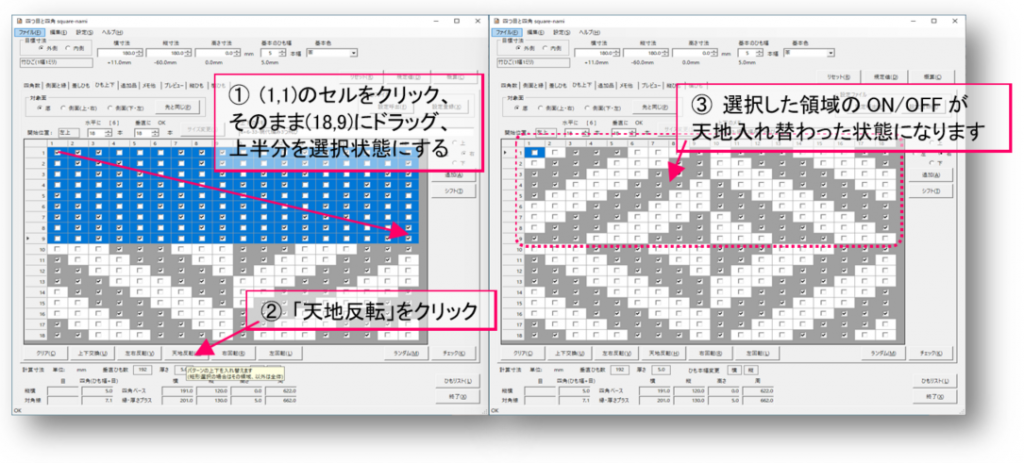
四方網代風の編み目になりました。プレビューで見てみましょう。

左は18×18の繰り返し、右は横ひもが等幅の図です。
左下1/4領域を選択して「上下交換」をクリックします。次に右上1/4領域を選択して再度「上下交換」をクリックします。
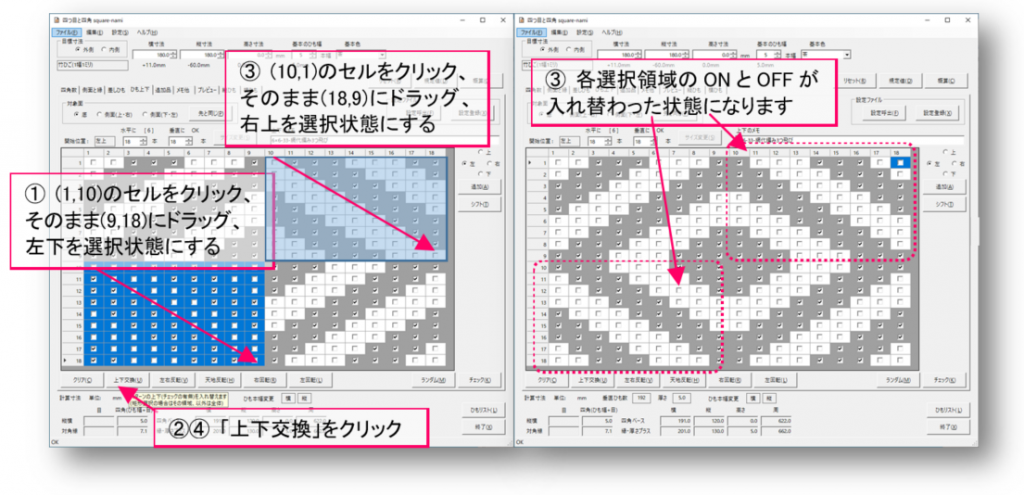
桝網代風の編み目になりました。プレビューで見てみましょう。

左は18×18の繰り返し、右は横ひもが等幅の図です。
上方向に9回シフトします。9行は18行の半分ですから、上半分と下半分がちょうど入れ替わります。
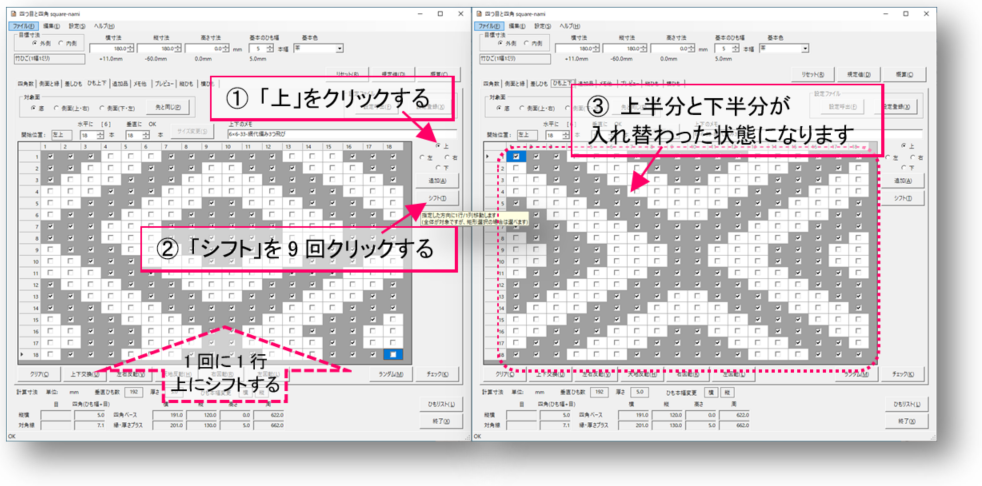
開き網代風の編み目になりました。プレビューで見てみましょう。

左は18×18の繰り返し、右は横ひもが等幅の図です。
垂直方向の繰り返し単位を18の半分、9にします。
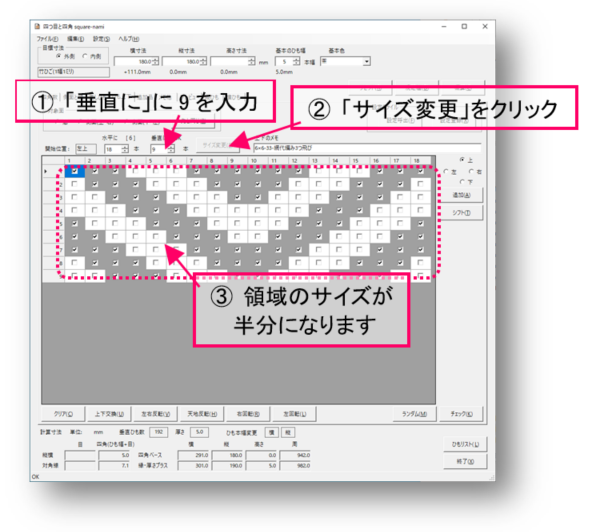
垂直方向では、同じ範囲に対して単位が2回適用されることになります。プレビューで見てみましょう。

左は、ひも幅は18×18・編み目は19×9の繰り返し、右は横ひもが等幅の図です。
下に5回シフトします。
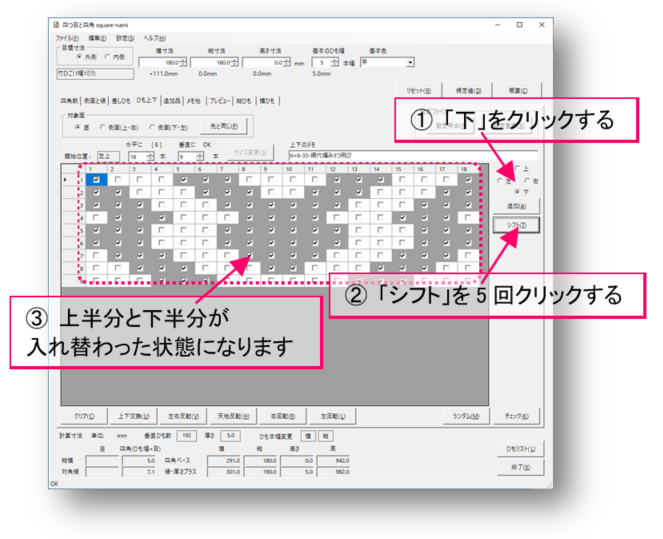
5行は9行の約半分ですから、ひも幅との位置関係を上下方向に約半分ずらすことになります。
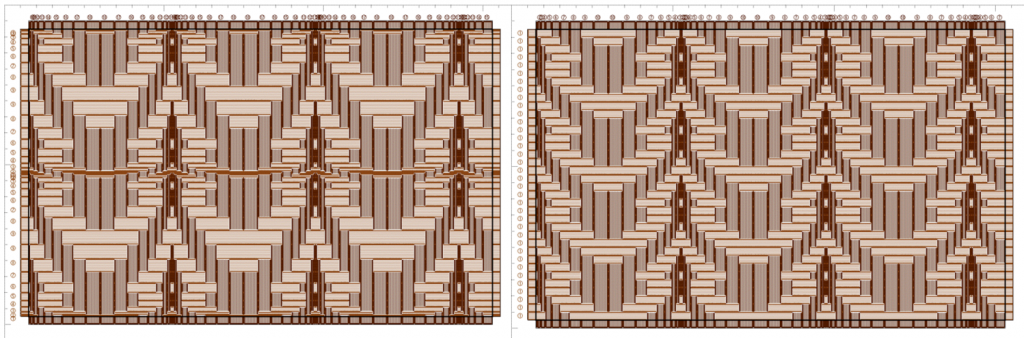
左図は、先の図と幅と編み目の位置関係がずれています。右図は等幅ですから同じになります。
まだ「模様」と呼べるほどのものではなく、繰り返し幅も、編み目も、改善の余地は大いにあります。でも、組み合わせを試すためのおおよその操作は、ご理解いただけたのではないでしょうか。