issue#98~#101に対応しました。
描画色に画像が登録可能に
[設定]メニューの[描画色]画面で画像が登録可能になりました。
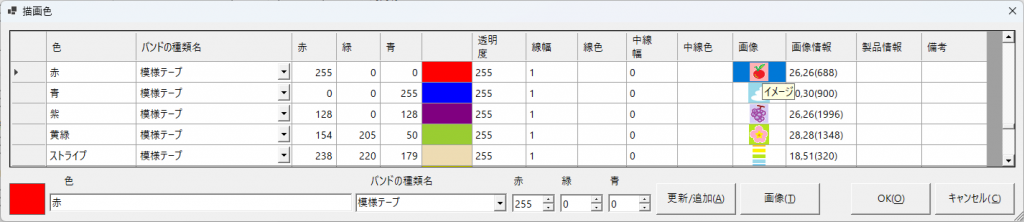
右から4列目に「画像」カラムが増えました。セルを選択し、画像ボタンからpngファイルを指定してください。半透明にしたい場合は、ペイント3Dなどのアプリで透明度を指定した画像を作ってください。
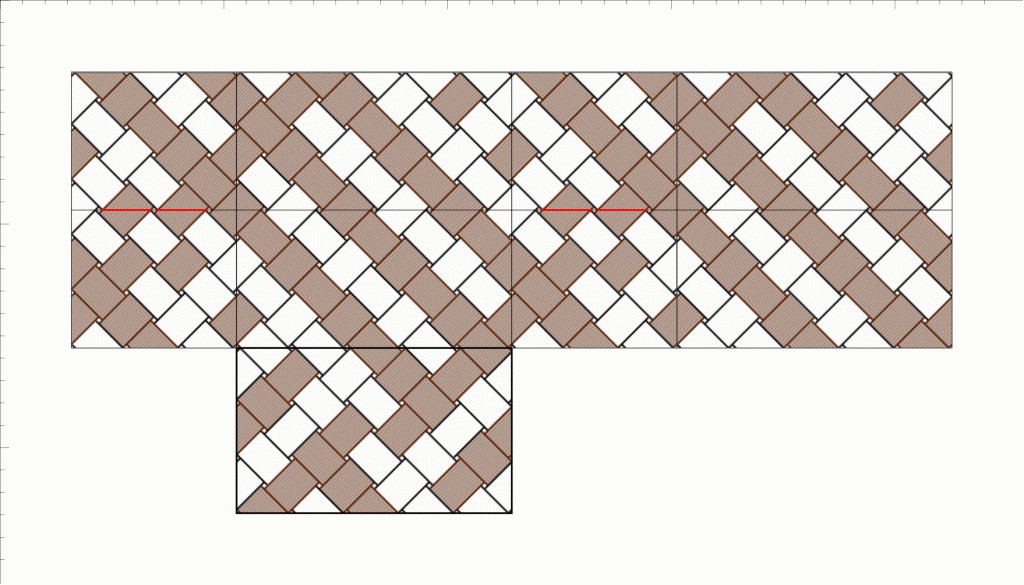
[バンドの種類]に対して、画像を登録した色を割り当てると、プレビュー時のバンド表示時に、指定した画像を敷き詰めた表示ができるようになります。メッシュワークで、布をテープ状に編んでパッチワークの模様を作ったことがありましたが、そのような時に便利かと思います。
ただし、画像のどの位置が表示されるかについては解像度などにより変わりますので、正確な画像表示というより、模様の目安程度とお考え下さい。また、登録可能なのは、小さい.png画像だけです。
squareとhexagonのプレビュー図の例です。

この例のバンドの種類「模様テープ」の設定ファイルです。
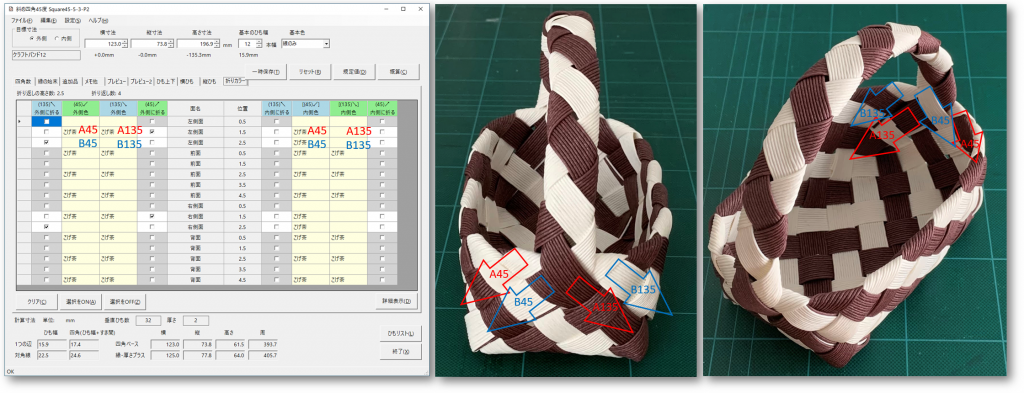
Square45の折りカラー機能修正
[プレビュー]画像表示のバグ修正と合わせて、45度と135度のバンド色が同じ場合、チェックボックスの背景をグレーにしました。チェックは可能ですが、折り返しても色が変わらない箇所が、見てわかるようになりました。
例えば以下は、「斜め編みの崩し縞のかご」のデータですが、「折りカラー編み」にチェックを入れることで、作りたい高さにおけるバンドの並びを確認することができます。左図、高さ10だと両方向全て同色なので、縁の始末を外側に折り返しても大丈夫ということがわかります。右図のように高さを9.5に変えると不一致箇所がでてきます。
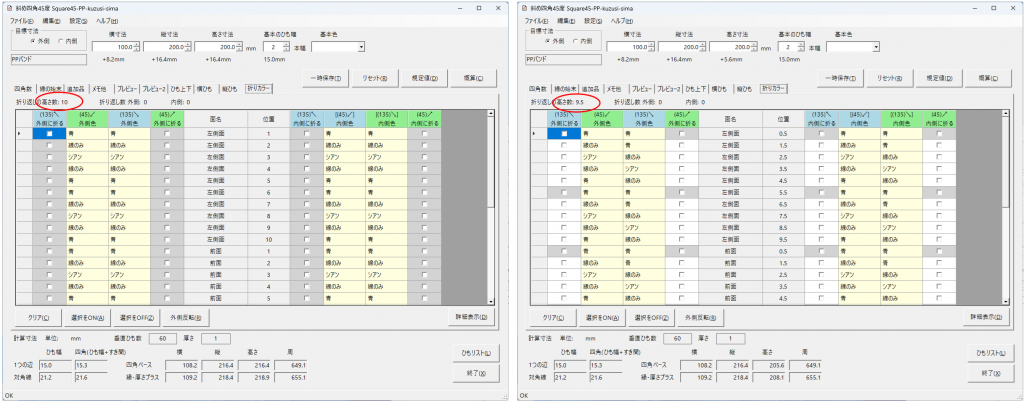
「折りカラー編み」にしない(最終的にはチェックを外す)場合でも、デザイン途中でオン/オフは可能ですから、高さ選択の参考などに使えるかと思います。
ダウンロードはこちら
Release v1.8.15 のリリース
※添付の設定ファイル CraftBandMesh.XML の変更点は以下。
- 描画色に、画像情報と画像文字列のフィールド追加(中身は全て空です)
- 白、deep白のRGB値を255・255・255から253・253・253 に変更(v1.8.14のフォローアップ)
- 編みかたに「ノコギリ状に折って差し込む(プラス8個)」を追加